Предмет: Геометрия,
автор: ГОСТЬ2014
В равнобедренной трапеции основания равны 3 см и 5 см ,а боковая сторона 7 см. Вычислите площадь трапеции
Ответы
Автор ответа:
0
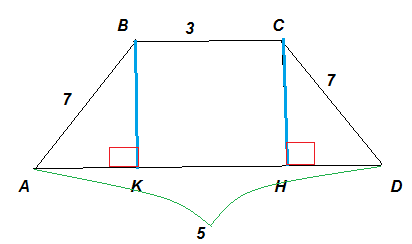
Дано: ABCD - равнобедренная трапеция, AB = CD =7 см. ВС = 3см, АD = 5см.
Найти:
Решение:
Так как трапеция равнобедренная, то боковые стороны равны и углы при основании также равны.
1) Так как КН = ВС =5 см, то AK = DH =
2) С прямоугольного треугольника ABK (угол AKB = 90градусов):
По т. ПИфагора определим высоту

3) Площадь трапеции равна полусумме оснований умноженное на высоту

Ответ:
Найти:
Решение:
Так как трапеция равнобедренная, то боковые стороны равны и углы при основании также равны.
1) Так как КН = ВС =5 см, то AK = DH =
2) С прямоугольного треугольника ABK (угол AKB = 90градусов):
По т. ПИфагора определим высоту
3) Площадь трапеции равна полусумме оснований умноженное на высоту
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mihailsmm
Предмет: Русский язык,
автор: danya070237
Предмет: Геометрия,
автор: Аноним
Предмет: История,
автор: Аноним
Предмет: Обществознание,
автор: legolubev