Предмет: Математика,
автор: heysss
Помогите пожалуйста! Решить ур-ние
Приложения:
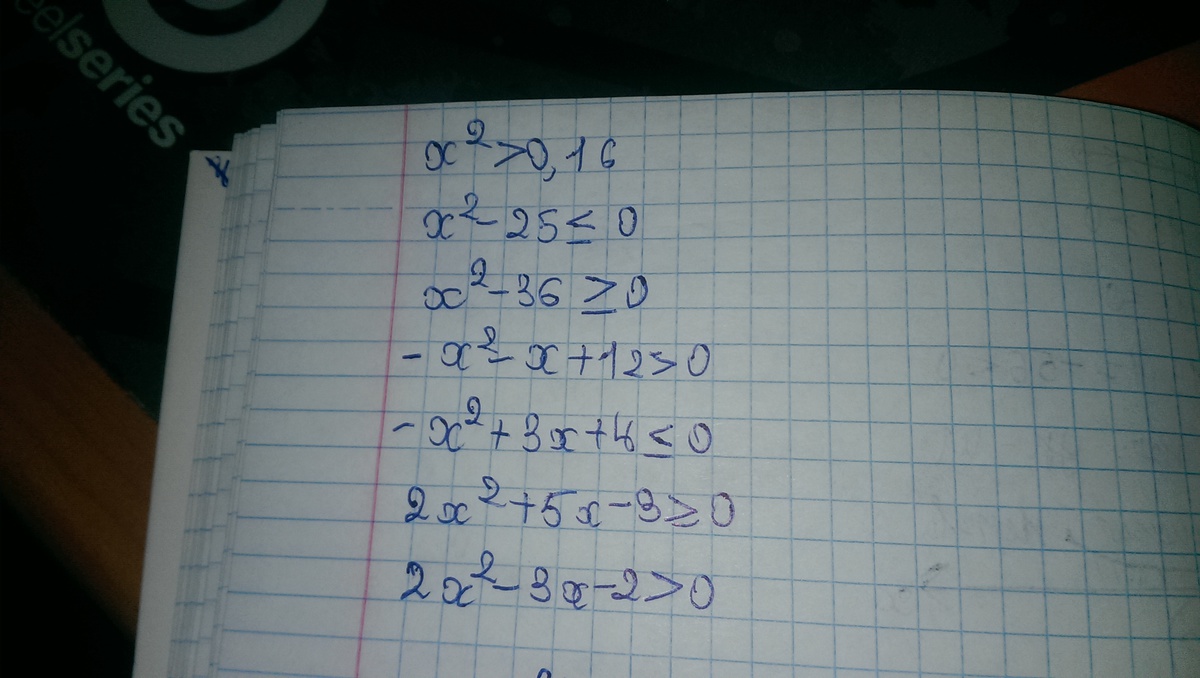
Ответы
Автор ответа:
0
х² ≥ 0,16
|x| ≥ 0,4
x ∈ (-oo ; -0,4] U [0,4 ; +oo)
х² - 25 ≤ 0
x² ≤ 25
|x| ≤ 5
x ∈ [-5 ; 5]
х² - 36 ≥ 0
x² ≥ 36
|x| ≥ 6
x ∈ (-oo ; -6] U [6 ; +oo)
-x² - x + 12 > 0
x² + x - 12 < 0
x² + x - 12 = 0
По теореме Виета: x₁ = -4; x₂ = 3
Парабола y = -x² - x + 12 идёт ветвями вниз и пересекает Ох в точках:
x₁ = -4; x₂ = 3.
х ∈ (-4 ; 3)
-x² + 3x + 4 ≤ 0
x² - 3x - 4 ≥ 0
x² - 3x - 4 = 0
По теореме Виета: x₁ = -1; x₂ = 4
Парабола y = -x² + 3x + 4 идёт ветвями вниз и пересекает Ох в точках:
x₁ = -1; x₂ = 4.
х ∈ (-оо ; -1] U [4 ; +oo)
2x² + 5x - 3 ≥ 0
2x² + 5x - 3 = 0
D = 5² - 4·2·(-3) = 49
x₁ = = -3
= -3
x₂ = =
= 
Парабола y = 2x² + 5x - 3 идёт ветвями вверх и пересекает Ох в точках:
x₁ = -3; x₂ = .
.
х ∈ (-оо ; -3] U [ ; +oo)
; +oo)
2x² - 3x - 2 > 0
2x² - 3x - 2 = 0
D = (-3)² - 4·2·(-2) = 25
x₁ = = -
= - 
x₂ = = 2
= 2
Парабола y = 2x² - 3x - 2 идёт ветвями вверх и пересекает Ох в точках:
x₁ = - ; x₂ = 2.
; x₂ = 2.
х ∈ (-оо ; - ) U (2 ; +oo)
) U (2 ; +oo)
|x| ≥ 0,4
x ∈ (-oo ; -0,4] U [0,4 ; +oo)
х² - 25 ≤ 0
x² ≤ 25
|x| ≤ 5
x ∈ [-5 ; 5]
х² - 36 ≥ 0
x² ≥ 36
|x| ≥ 6
x ∈ (-oo ; -6] U [6 ; +oo)
-x² - x + 12 > 0
x² + x - 12 < 0
x² + x - 12 = 0
По теореме Виета: x₁ = -4; x₂ = 3
Парабола y = -x² - x + 12 идёт ветвями вниз и пересекает Ох в точках:
x₁ = -4; x₂ = 3.
х ∈ (-4 ; 3)
-x² + 3x + 4 ≤ 0
x² - 3x - 4 ≥ 0
x² - 3x - 4 = 0
По теореме Виета: x₁ = -1; x₂ = 4
Парабола y = -x² + 3x + 4 идёт ветвями вниз и пересекает Ох в точках:
x₁ = -1; x₂ = 4.
х ∈ (-оо ; -1] U [4 ; +oo)
2x² + 5x - 3 ≥ 0
2x² + 5x - 3 = 0
D = 5² - 4·2·(-3) = 49
x₁ =
x₂ =
Парабола y = 2x² + 5x - 3 идёт ветвями вверх и пересекает Ох в точках:
x₁ = -3; x₂ =
х ∈ (-оо ; -3] U [
2x² - 3x - 2 > 0
2x² - 3x - 2 = 0
D = (-3)² - 4·2·(-2) = 25
x₁ =
x₂ =
Парабола y = 2x² - 3x - 2 идёт ветвями вверх и пересекает Ох в точках:
x₁ = -
х ∈ (-оо ; -
Похожие вопросы
Предмет: История,
автор: nikitamarcenko49
Предмет: Английский язык,
автор: buglakovaalion
Предмет: Биология,
автор: surum695
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: kazakbaymuhamm