Question

В равнобедренном треугольнике углы при вершине равны α,высота,опущенная на боковую сторону равна h.Найти стороны треугольника

Answer 1

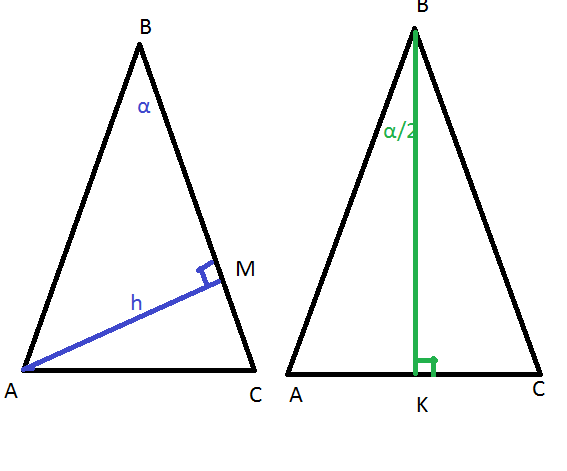
 В прямоугольном треугольнике АВМ ( cм. рис.1)
: катет АМ=h. ∠АВМ=α
По определению
 sinα=h/AB⇒  AB=h/sinα
См. рис.2
Высота равнобедренного треугольника является и биссектрисой и медианой
Поэтому она делит угол α пополам и сторону АС пополам:
АК=КС
Из прямоугольного треугольника АВК:
sin (α/2)=AK/AB  ⇒    AK = AB·sin(α|2)=h·sin(α/2)/sinα
AC = AK + KC = AK + AK= 2h·sin(α/2)/sinα=h/cos(α/2)
применили формулу sinα = 2·sin(α/2)·cos(α/2)
Ответ. АВ=ВС=h/sinα  - боковые стороны
           АС=h/cos(α/2)  - основание

Answer 2

Боковые стороны равны АВ = ВС = h / sin α.
Основание равно 2*АВ*sin (α/2) = 2*h*sin (α/2) / sin α