Question

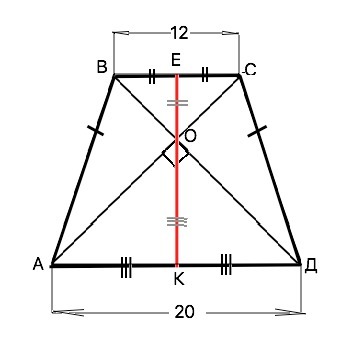
В равнобедренной трапеции основания равны 12 см и 20 см, а диагонали взаимно перпендикулярны. Вычислите площадь трапеции.

Answer 1

Площадь трапеции равна произведению высоты на полусумму оснований. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований. h=(BC+AD):2 ⇒ h(ABCD)=(12+20):2=16 см. S(ABCD)=h•(12+20):2=16•16=256 см².

Подробнее:  В равнобедренной трапеции диагонали равны. Точкой пересечения они делятся пополам и образуют с основаниями равнобедренные прямоугольные треугольники. Высота каждого из них - медиана и равна половине гипотенузы (соответствующего основания трапеции). ОЕ=ВС/2, ОК=AD/2 Высота трапеции h=ЕК=ЕО+ОК. EK=ВС/2+АD:2, т.е.h= (ВС+AD):2 ⇒S=16•16=256 см²