Предмет: Геометрия,
автор: toloshnaya99
В равнобедренной трапеции меньшее основание равно боковой стороне, а большее основание равно диагонали. Вычислите углы трапеции.
Ответы
Автор ответа:
0
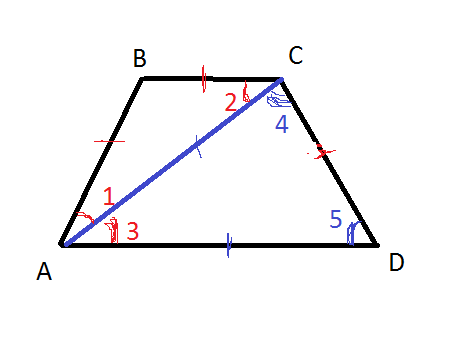
Треугольник АВС - равнобедренный, так как АВ= ВС
Значит ∠1 = ∠ 2
∠2 = ∠ 3 как внутренние накрест лежащие углы при параллельных прямых BC и AD.
Значит ∠1 = ∠ 2 = ∠ 3
Пусть ∠1 = ∠ 2 = ∠ 3 = х°
Треугольник АСD - равнобедренный, так как АC= AD
Значит ∠4 = ∠ 5
Так как сумма углов прилежащих к боковой стороне трапеции равна 180°, то
∠С + ∠ D = 180°
x° + ∠4 + ∠ 5 = 180°
x° + ∠4 + ∠ 4 = 180° ⇒2· ∠ 4 = 180°- x° ⇒∠ 4 = (180°- x° )/2
Так как углы при основании равнобедренной трапеции равны,
∠А = ∠ D
x° + x° = ∠5, ∠ 4 = ∠5
2х° = (180°- x° )/2
4х°= 180° - х°
5х°=180,
х°=36°
Значит ∠1 = ∠ 2 = ∠ 3 =36° , ∠ 4 = ∠5 =(180°-36°)/2=72°
∠ A = ∠1 +∠3 = 36°+36°= 72° , ∠ B = 180°-72°=108°
Ответ. ∠ A = ∠ D =72° , ∠ B = ∠C =180°-72°=108°
Значит ∠1 = ∠ 2
∠2 = ∠ 3 как внутренние накрест лежащие углы при параллельных прямых BC и AD.
Значит ∠1 = ∠ 2 = ∠ 3
Пусть ∠1 = ∠ 2 = ∠ 3 = х°
Треугольник АСD - равнобедренный, так как АC= AD
Значит ∠4 = ∠ 5
Так как сумма углов прилежащих к боковой стороне трапеции равна 180°, то
∠С + ∠ D = 180°
x° + ∠4 + ∠ 5 = 180°
x° + ∠4 + ∠ 4 = 180° ⇒2· ∠ 4 = 180°- x° ⇒∠ 4 = (180°- x° )/2
Так как углы при основании равнобедренной трапеции равны,
∠А = ∠ D
x° + x° = ∠5, ∠ 4 = ∠5
2х° = (180°- x° )/2
4х°= 180° - х°
5х°=180,
х°=36°
Значит ∠1 = ∠ 2 = ∠ 3 =36° , ∠ 4 = ∠5 =(180°-36°)/2=72°
∠ A = ∠1 +∠3 = 36°+36°= 72° , ∠ B = 180°-72°=108°
Ответ. ∠ A = ∠ D =72° , ∠ B = ∠C =180°-72°=108°
Приложения:
Автор ответа:
0
Пожалуйста))
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Биология,
автор: Vitya12345678887
Предмет: Физика,
автор: DashaSafronov
Предмет: Литература,
автор: Elishka2001