Предмет: Геометрия,
автор: stirexx
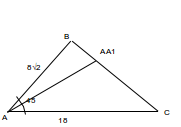
В треугольнике ABC стороны AB = 8 корень из двух AC = 18 и угол BAC = 45. Вычислите медиану АА1
Ответы
Автор ответа:
0
Дано: ABC - треугольник АВ = 8√2, АС = 18, Угол ВАС =45°.
Найти: АА₁.
Решение:
По т. косинусов определим третью сторону ВС


Определим медиану АА₁

Ответ: АА₁ = √185
Найти: АА₁.
Решение:
По т. косинусов определим третью сторону ВС
Определим медиану АА₁
Ответ: АА₁ = √185
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ziyaviddinovak
Предмет: Литература,
автор: obivalinaalex
Предмет: Музыка,
автор: Aksana761
Предмет: Математика,
автор: vladislavastyles
Предмет: Литература,
автор: Масяня1029