Предмет: Алгебра,
автор: css101
sin6x-sin3x=0 Решить уравнение. Ответ дать в градусах. Вроде бы простое, но я что-то не могу сообразить.
Ответы
Автор ответа:
0
ДУМАЕМ
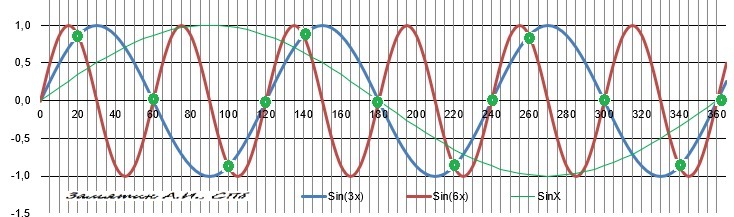
Применим ГРАФИЧЕСКИЙ метод решения уравнений.
ДАНО
Sin(6*x) = Sib(3*x)
Графики строим методом последовательного преобразования.
АЛГОРИТМ решения.
1. График Y= Sin(x)
2. График Y = Sin(3*x) - "сжат" по оси Х в ТРИ раза.
3. График Y = Sin(6*x) - "сжат" по оси Х в ШЕСТЬ раз.
Рисунок с графиками в приложении.
4. Находим точки пересечения нужных нам графиков и...... ВИДИМ, что можно уже перейти к ответу.
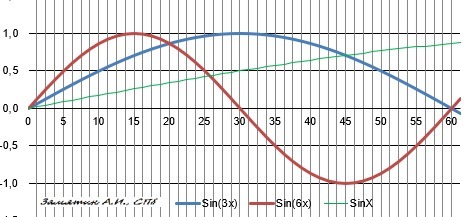
Первая группа точек пересечения - прямо на оси Х и через 60° (π/3) - ОТВЕТ 1) 60°.
Это точки кратные коэффициентам 6х и 3х в уравнении.
Но видим и вторую группу точек пересечения и они уже не на оси Х.
И, скорее всего, эти точки кратны - 6*3 = 18х.
И это будет...
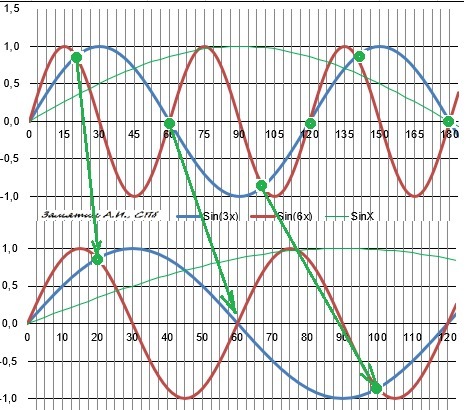
Увеличили точность построения графика.
360° : 18 = 20°, но с периодом в 80°.
ОТВЕТ 2) 20°+, 100-, 140+, 220- и далее с периодом 360°
Остаётся объединить три ответа за период в 360° в одном.
ОТВЕТ: 0°, 20°, 60°, 100°, 120°, 140°,180°, 220°, 240°, 260°, 300°, 340°.
И решено и ни одной тригонометрической формулы.
Применим ГРАФИЧЕСКИЙ метод решения уравнений.
ДАНО
Sin(6*x) = Sib(3*x)
Графики строим методом последовательного преобразования.
АЛГОРИТМ решения.
1. График Y= Sin(x)
2. График Y = Sin(3*x) - "сжат" по оси Х в ТРИ раза.
3. График Y = Sin(6*x) - "сжат" по оси Х в ШЕСТЬ раз.
Рисунок с графиками в приложении.
4. Находим точки пересечения нужных нам графиков и...... ВИДИМ, что можно уже перейти к ответу.
Первая группа точек пересечения - прямо на оси Х и через 60° (π/3) - ОТВЕТ 1) 60°.
Это точки кратные коэффициентам 6х и 3х в уравнении.
Но видим и вторую группу точек пересечения и они уже не на оси Х.
И, скорее всего, эти точки кратны - 6*3 = 18х.
И это будет...
Увеличили точность построения графика.
360° : 18 = 20°, но с периодом в 80°.
ОТВЕТ 2) 20°+, 100-, 140+, 220- и далее с периодом 360°
Остаётся объединить три ответа за период в 360° в одном.
ОТВЕТ: 0°, 20°, 60°, 100°, 120°, 140°,180°, 220°, 240°, 260°, 300°, 340°.
И решено и ни одной тригонометрической формулы.
Приложения:
Автор ответа:
0
Решение при помощи формул на приложенном изображении.
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: DmitriyMOKEEV
Предмет: Литература,
автор: 123458967483
Предмет: Українська мова,
автор: ksiushkaprima
Предмет: Алгебра,
автор: alserpoc