Предмет: Геометрия,
автор: 98kate9898
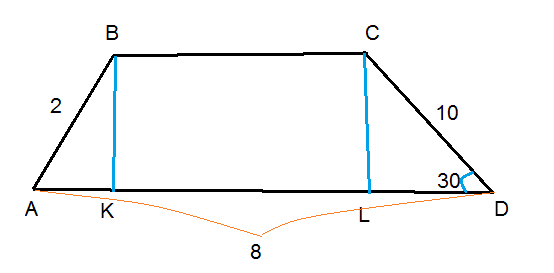
Дана трапеция ABCD. AB=2cm, CD=10cm, DA=8cm, угол D=30 градусов. Найти площадь трапеции.
Ответы
Автор ответа:
0
ABCD - трапеция, AB = 2см, CD = 10см, AD = 8см. угол D = 30 Градусов
Найти:
Решение:
Проведем высоты BK и CL к стороне основанию AD. С прямоугольного треугольника CDL (угол CLD = 90 градусов), по т. Пифагора ищем DL и высоту CL
Синус угла - это отношение противолежащего катета к гипотенузе, тоесть


Также определим АК (с прямоугольного треугольника АКВ)
Косинус угла это отношение прилежащего катета к гипотенузе, тоесть

Тогда меньшее основание ВС равен:

Вычисляем площадь трапеции

Ответ:
Найти:
Решение:
Проведем высоты BK и CL к стороне основанию AD. С прямоугольного треугольника CDL (угол CLD = 90 градусов), по т. Пифагора ищем DL и высоту CL
Синус угла - это отношение противолежащего катета к гипотенузе, тоесть
Также определим АК (с прямоугольного треугольника АКВ)
Косинус угла это отношение прилежащего катета к гипотенузе, тоесть
Тогда меньшее основание ВС равен:
Вычисляем площадь трапеции
Ответ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: kolonkaden
Предмет: Математика,
автор: ysadovii
Предмет: Геометрия,
автор: truptrap00
Предмет: Информатика,
автор: nastik2002kot
Предмет: Обществознание,
автор: Дамbhjr