Предмет: Алгебра,
автор: jeny16
Помогите решить:
1)сколько корней имеет уравнение sinx+cosx=1 на отрезке [-п;2п]
2)сколько корей имеет уравнение tgx+1/tgx=2 на отрезке [-2п;п]
3)сколько корней уравнениz sin3x+sin5x=sin4x удовлетворяют неравенству
( модуль x) /x/<=п/2
4) сколько корней имеет уравнение 3sin5x+4cos5x=6 на промежутке [-п;2п]
Ответы
Автор ответа:
0
На отрезке [-π; 2π]:
0, π/2, 2π, то есть три корня.
На отрезке [-2π; π]:
-7π/4, -3π/4, π/4, то есть три корня.
3. На фотке
4. На фотке (0 корней)
Приложения:
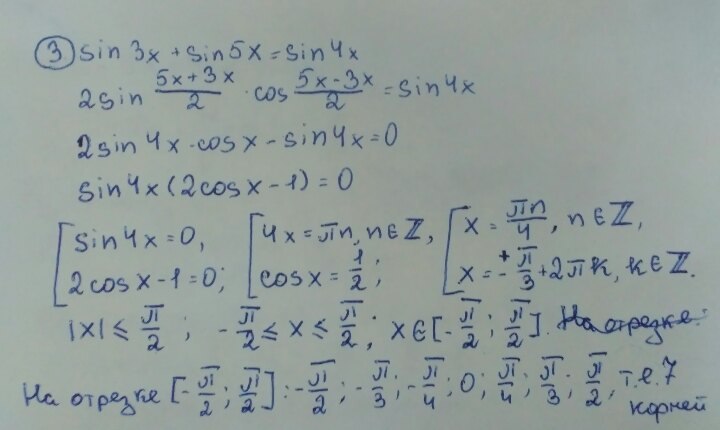

Похожие вопросы
Предмет: Українська мова,
автор: ivanovadaria53
Предмет: Геометрия,
автор: tamapa7354
Предмет: Алгебра,
автор: 960225400782iin
Предмет: Математика,
автор: НаsTyouшКa