Предмет: Алгебра,
автор: k24ristina1
Докажите, что значение выражения является иррациональным
Приложения:
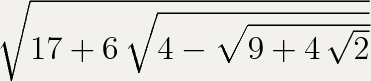
Ответы
Автор ответа:
0
а значит иррациональное как сумма рационального числа 3 и иррационального
Похожие вопросы
Предмет: Другие предметы,
автор: Sasha5868
Предмет: Обществознание,
автор: mcdima228
Предмет: Английский язык,
автор: zopovpeta408
Предмет: Геометрия,
автор: raskatov201