Предмет: Алгебра,
автор: Me00007
Решить три примера из файла с ПОДРОБНЫМ решением!
Приложения:
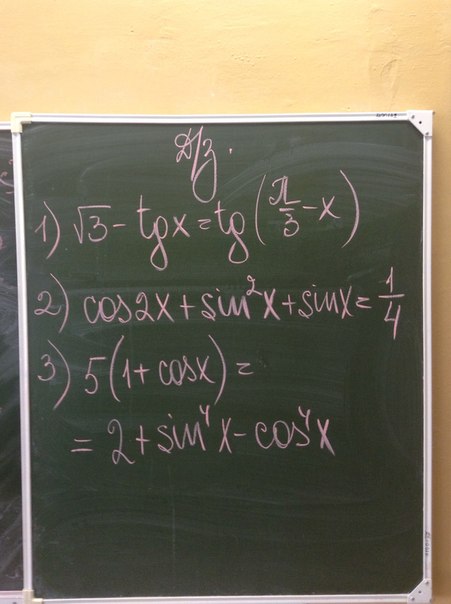
Ответы
Автор ответа:
0
1)√3-tgx=tg(π/3)
tg(π/3-x)=(tgπ/3-tgx)/(1+tgπ/3tgx)=(√3-tgx)/(1+√3tgx)
√3-tgx=(√3-tgx)/(1+√3tgx)
(√3-tgx)-(√3-tgx)/(1+√3tgx)=0
[(√3-tgx)(1+√3tgx)-(√3-tgx)]/(1+√3tgx)=0
1+√tgx≠0⇒tgx≠-1/√3⇒x≠-π/6+πn
(√3-tgx)(1+√3tgx-1)=0
√3tgx(√3-tgx)=0
tgx=0⇒x=πn
tgx=√3⇒x=π/3+πn
2)cos2x+sin²x+sinx=1/4
1-2sin²x+sin²x+sinx=1/4
sin²x-sinx-3/4=0
sinx=a
4a²-4a-3=0
D=16+48=64
a1=(4-8)/8=-1/2⇒sinx=-1/2⇒x=(-1)^n+1 *π/6+πn
a2=(4+8)/8=1,5∉[-1;1]
3)5(1+cosx)=2+
5(1+cosx)=2+(sin²x-cos²x)(sin²x+cos²x)
5(1+cosx)=2+(sin²x-cos²x)
5(1+cosx)=2+1-2cos²x
2cos²x+5cosx+2=0
cosx=a
2a²+5a+2=0
D=25-16=9
a1=(-5-3)/4=-2∉[-1;1]
a2=(-5+3)/4=-1/2⇒cosx=-1/2⇒x=+-2π/3+2πn
tg(π/3-x)=(tgπ/3-tgx)/(1+tgπ/3tgx)=(√3-tgx)/(1+√3tgx)
√3-tgx=(√3-tgx)/(1+√3tgx)
(√3-tgx)-(√3-tgx)/(1+√3tgx)=0
[(√3-tgx)(1+√3tgx)-(√3-tgx)]/(1+√3tgx)=0
1+√tgx≠0⇒tgx≠-1/√3⇒x≠-π/6+πn
(√3-tgx)(1+√3tgx-1)=0
√3tgx(√3-tgx)=0
tgx=0⇒x=πn
tgx=√3⇒x=π/3+πn
2)cos2x+sin²x+sinx=1/4
1-2sin²x+sin²x+sinx=1/4
sin²x-sinx-3/4=0
sinx=a
4a²-4a-3=0
D=16+48=64
a1=(4-8)/8=-1/2⇒sinx=-1/2⇒x=(-1)^n+1 *π/6+πn
a2=(4+8)/8=1,5∉[-1;1]
3)5(1+cosx)=2+
5(1+cosx)=2+(sin²x-cos²x)(sin²x+cos²x)
5(1+cosx)=2+(sin²x-cos²x)
5(1+cosx)=2+1-2cos²x
2cos²x+5cosx+2=0
cosx=a
2a²+5a+2=0
D=25-16=9
a1=(-5-3)/4=-2∉[-1;1]
a2=(-5+3)/4=-1/2⇒cosx=-1/2⇒x=+-2π/3+2πn
Похожие вопросы
Предмет: Математика,
автор: foxlana550
Предмет: География,
автор: irinagavazina43
Предмет: Физкультура и спорт,
автор: davidsona
Предмет: Информатика,
автор: jeniferlopez