Предмет: Алгебра,
автор: muslimkakz97
Решите неравенство(x-2)(x+3)(x-1)^2больше или равно 0; |х-2|(х+4)(х-5)^2меньше или равно 0.
Ответы
Автор ответа:
0
Ответ:
решение представлено на фото
Объяснение:
Приложения:
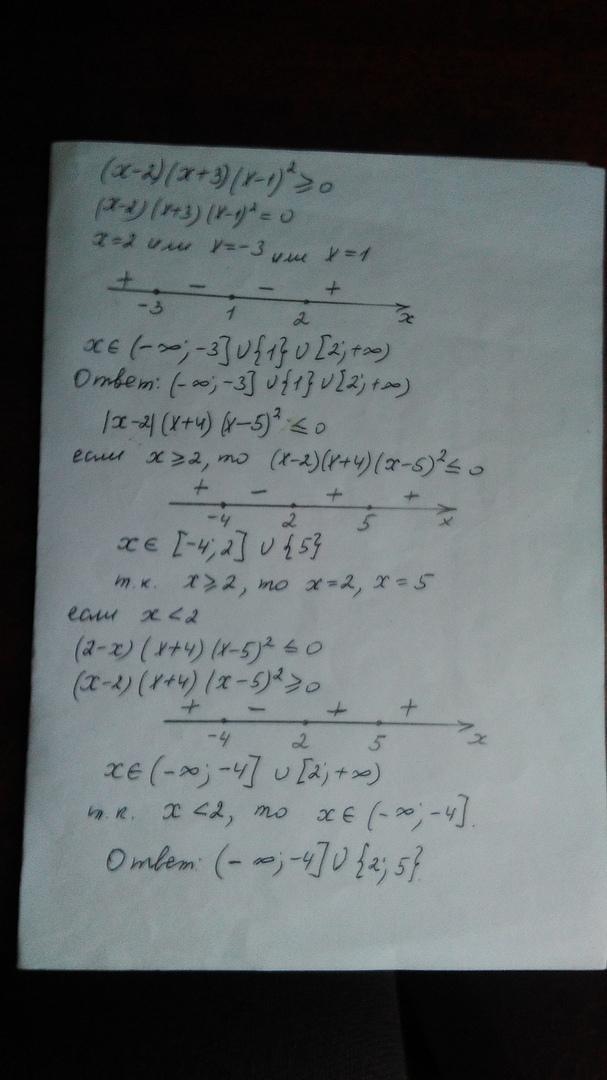
Автор ответа:
0
ОДЗ неравенства - множество действительных чисел.
Приравниваем неравенство к нулю, получим
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю
____+__[-3]____-___[1]___-____[2]____+___
Ответ:
Аналогично ОДЗ неравенства - множество всех действительных чисел.
Приравниваем неравенство к нулю, имеем
___-___[-4]___+__[2]____+___[5]___+____
Ответ:
Приложения:
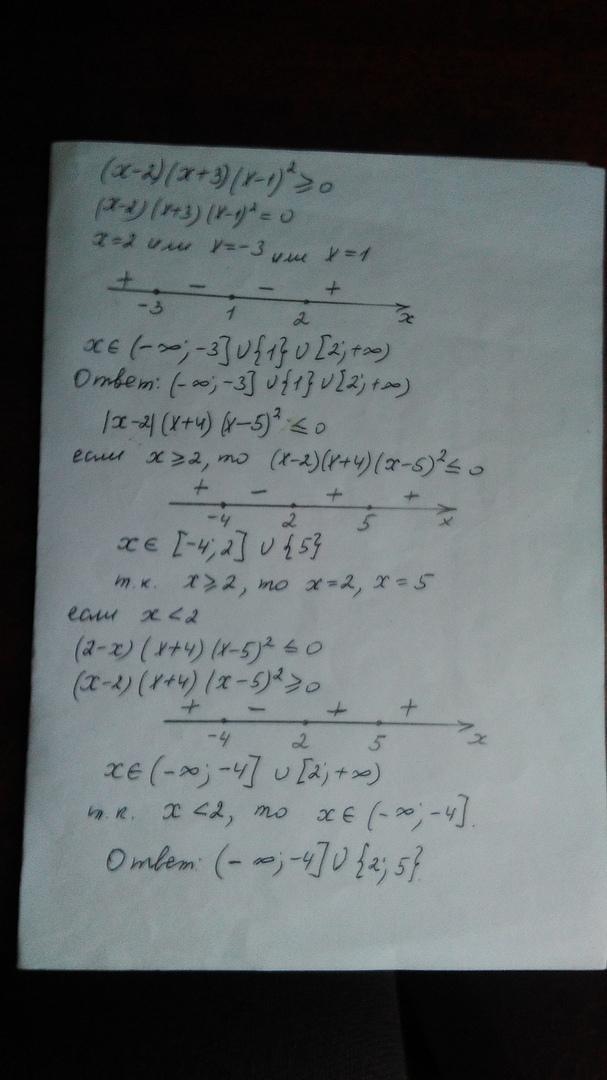
Похожие вопросы
Предмет: География,
автор: kristinabutnotsi
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: dinaheppy
Предмет: Химия,
автор: yмHuk
Предмет: Литература,
автор: stepaniansiuzan