Question

Вывести формулу объема усеченной конуса. Через интеграл. С графиком.

Answer 1

Итак, попробую еще раз, я тебе уже показывал как выводится формула объема конуса через интеграл, надеюсь там все понятно.
Чтобы вывести объем усеченного конуса, мы рассмотрим его как разность объема полного конуса и объема отсеченного конуса. 
Итак, Vус=Vпол-Vотс
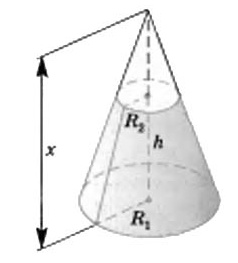
Пусть в нашем усеченном конусе h-высота, r2 и r1 - радиусы верхнего и нижнего основания соответственно. рисунок во вложении.
Пусть высота полного х, тогда высота отсеченного х-h, из подобия этих конусов получим:
х/(x-h)=r1/r2
x=hr1/(r1-r2)
V=1/3·π·x·r1²-1/3·π(x-h)·r2²
Объемы этих двух конусов через интеграл я уже тебе показывал!
После подстановки и упрощения получим:
V=1/3·π·h(r1²+r1·r2+r2²)