Предмет: Алгебра,
автор: masha993
Решить систему уравнений.
Приложения:
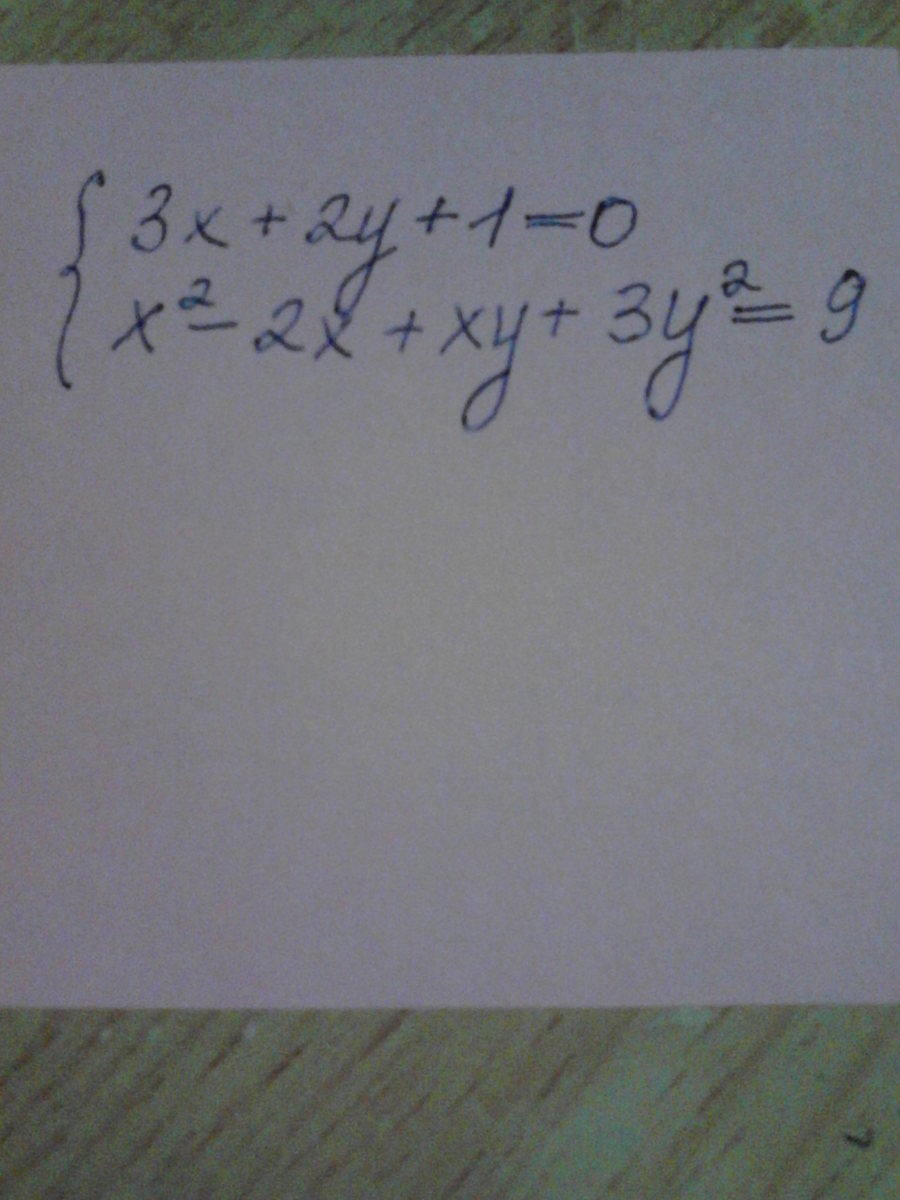
Ответы
Автор ответа:
0
Автор ответа:
0
Используем метод подстановки:
из первого уравнения у = (-3х-1) / 2 подставляем во второе:
х²-2х+((х(-3х-1)) / 2)+((3(-3х-1)² / 4)=9
Приводим к общему знаменателю и приводим подобные:
25х²+8х-33 = 0 Д = 3364 √Д = 58 х₁ = 1 х₂ = -1,32
Подставив в первое уравнение получаем:
у₁ = -2 у₂ = 1,48
из первого уравнения у = (-3х-1) / 2 подставляем во второе:
х²-2х+((х(-3х-1)) / 2)+((3(-3х-1)² / 4)=9
Приводим к общему знаменателю и приводим подобные:
25х²+8х-33 = 0 Д = 3364 √Д = 58 х₁ = 1 х₂ = -1,32
Подставив в первое уравнение получаем:
у₁ = -2 у₂ = 1,48
Похожие вопросы
Предмет: Информатика,
автор: AvroraStar
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: HlowKity
Предмет: Математика,
автор: Аноним