Предмет: Алгебра,
автор: fkn0w3d
Решите системы уравнений :(
a) {x+2y=3 {4^(x-2,5)/4^3y=2
б){3^(x)*2^(y)=1/9 {y-x=2
в){5^(2x+1)>6,25 {11^(6x^2-10x)=11^(9x-15)
Приложения:

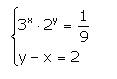
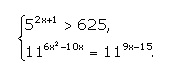
Ответы
Автор ответа:
0
Система номер 2
Корень х = 1,5 - не удовлетворяет неравенству
Ответ:
Автор ответа:
0
1) Для начала преобразуем второе уравнение системы.




Теперь система выглядит так:
 Вычтем из первого уравнения второе и получим:
Вычтем из первого уравнения второе и получим:  ⇒
⇒ 
Подставим в любое из уравнений и получаем
Ответ: (3;0)
2)

Подставим значение у во второе уравнение:


 , тогда y=x+2=-2+2=0
, тогда y=x+2=-2+2=0
Ответ: (-2;0)
3) Неравенство: 5^(2x+1) > 625
5^(2x+1) > 5^4
2x+1 > 4
x > 1.5
Уравнение:


D=b²-4ac=19²-4*6*15=361-360=1


C учетом неравенства подходит только второй корень:
Ответ:
Теперь система выглядит так:
Подставим в любое из уравнений и получаем
Ответ: (3;0)
2)
Подставим значение у во второе уравнение:
Ответ: (-2;0)
3) Неравенство: 5^(2x+1) > 625
5^(2x+1) > 5^4
2x+1 > 4
x > 1.5
Уравнение:
D=b²-4ac=19²-4*6*15=361-360=1
C учетом неравенства подходит только второй корень:
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: taisiiaburik
Предмет: Физика,
автор: Лиизаветка