Предмет: Геометрия,
автор: MoldyBread
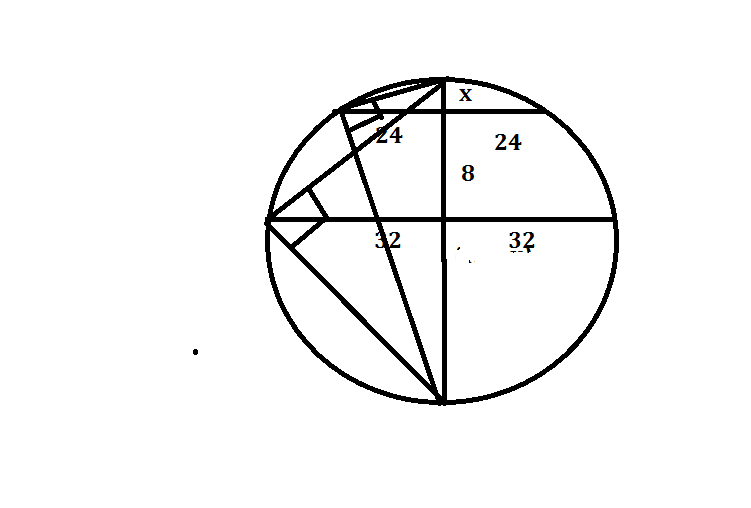
В круге по один бок от центра проведены 2 параллельные хорды, длины которых 48 и 64 см, а расстояние между ними 8 см. Найти Диаметр круга.
Ответы
Автор ответа:
0
Проведем второй диаметр перпендикулярный этим хордам.
В силу симметрии он делит их пополам. То обозначенные углы прямые тк опираются на диаметр. Причем выходит что полухорды являются высотами полученных прямоугольных треугольников.
То по теореме высоты:
24^2=x*(2R-x)=2Rx-x^2
32^2=(x+8)(2R-x-8)=2Rx-x^2-8x+16R-8x-64=2Rx-x^2-16x+16R-64
Вычетаем:
32^2-24^2=16(R-x)-64
28=R-x-4
x=R-32
576=(R-32)(R+32)
576=R^2-1024
R^2=1600
R=40
В силу симметрии он делит их пополам. То обозначенные углы прямые тк опираются на диаметр. Причем выходит что полухорды являются высотами полученных прямоугольных треугольников.
То по теореме высоты:
24^2=x*(2R-x)=2Rx-x^2
32^2=(x+8)(2R-x-8)=2Rx-x^2-8x+16R-8x-64=2Rx-x^2-16x+16R-64
Вычетаем:
32^2-24^2=16(R-x)-64
28=R-x-4
x=R-32
576=(R-32)(R+32)
576=R^2-1024
R^2=1600
R=40
Приложения:
Автор ответа:
0
Кстати задача не плотностью решена, Вы забыли про диаметр ))
Автор ответа:
0
Ах ну да :)
Автор ответа:
0
D=80 ясен пень
Похожие вопросы
Предмет: Информатика,
автор: Аноним
Предмет: Математика,
автор: artesbot
Предмет: Математика,
автор: Corvuscorone
Предмет: Геометрия,
автор: anasdeni
Предмет: Биология,
автор: сонятяпа