Question

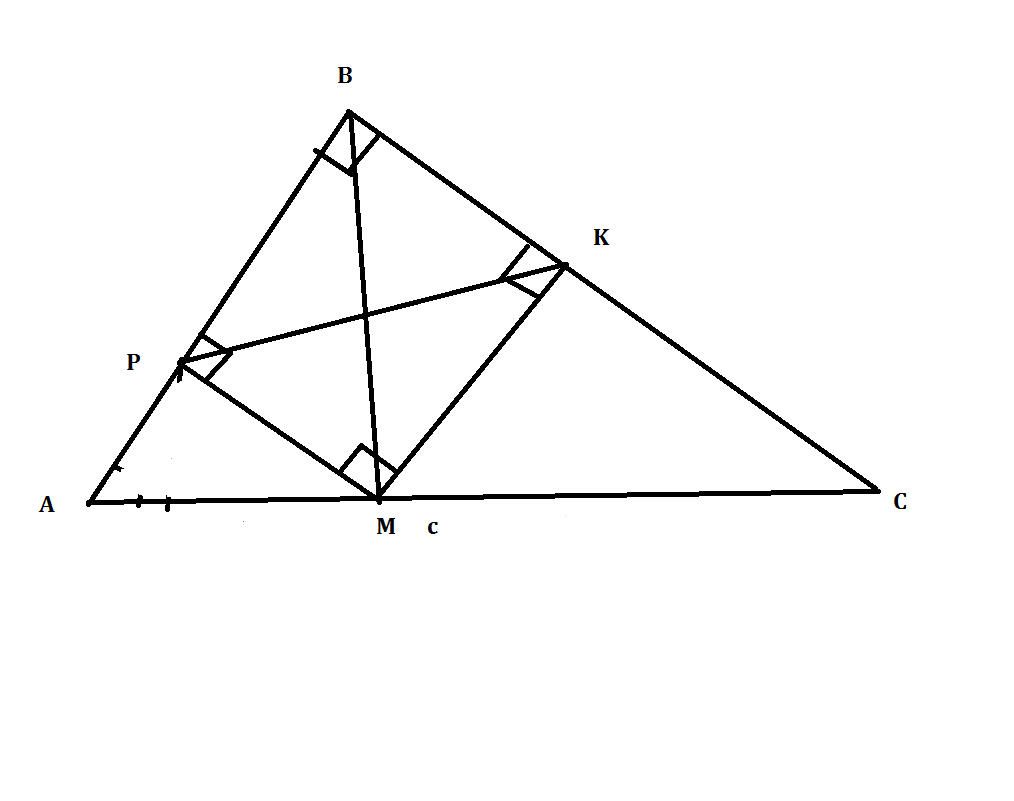
На гипотенузе прямоугольного треугольника выбрана произвольная точка , и из нее опущены перпендикуляры на катеты этого треугольника. Определите, при каком положении точки длина отрезка будет наименьшей.

Answer 1

Чисто геометрически   задача решается   легко.
4  угол  четырехугольника PBKM равен   360-90*3=90.
Таким образом PBKM-прямоугольник.
Проведем вторую диагональ   прямоугольника  BM.
То  BM=PK (как  диагонали прямоугольника)
ТО наименьшая PK  будет   при наименьшей BM.
А  длинна отрезка BM,является наименьшей  когда является высотой. (тк перпендикуляр  всегда меньше наклонной)
Таким образом  для нахождения этой точки  достаточно провести высоту прямого угла треугольника.  Пересечение высоты и гипотенузы и есть  данная точка.
Все гениальное  просто :)