Question

Точки M, N и P лежат на сторонах АВ, ВС, АС треугольника АВС, причем
AM/AB=  BN /BC=  CP /CA = 1/ 3 . Прямые СМ, AN, BP, пересекаясь, ограничивают
треугольник, площадь которого равна S. Найдите площадь треугольника ABC

Answer 1

       Положим что треугольник  $LKG$   площадь  котрого равна  $S$   

По теореме Менелая , получим   соотношения   $frac{AK}{KN} = frac{CG}{GM}=frac{BL}{LP} = frac{3}{4}$ 

$frac{BG}{GP}=frac{AL}{LN}=frac{CK}{KM}=6$

Допустим угол между сторонами меньшего треугольника равны $a,b,c$

 $KL=frac{3AN}{7}$

 $LG=frac{3BP}{7}$

 $LG=frac{3CM}{7}$

$frac{frac{9AN*BP}{49}*sina}{2}=S$       

$frac{frac{3*BP*6AN}{49}*sina}{2}=2S$

То есть площадь треугольника

$S_{ABC}=7S$

        

Answer 2

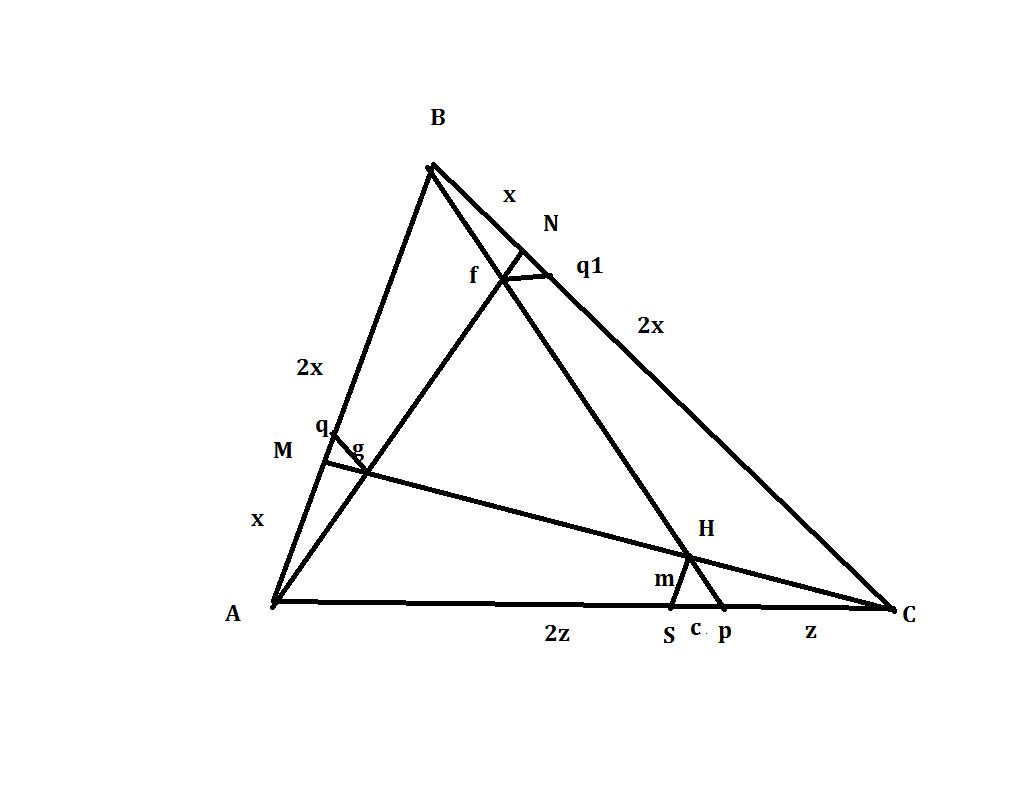
Проведем HS || AB. Обозначим   SH=m SP=c
треугольники AMC и SHC подобны как и треугольники ABP  и SHP.
Дальше просто поиграем с отношениями:
x/m=3z/(z+c)
3x/m=2z/c
поделим одно на второе:
3=2/c * (z+c)/3=2(z+c)/3c
 9c=2z+2c
2z=7c
c=2z/7
MC/HC=3z/(z+c)=3z/(z+2z/7)=3/(9/7))=7/3
Ну еще  для достижения успеха нужно найти  отношения:
BH/Hf и MH/Hg. В  целом это та же  игра отношений. Хотя иногда эта  игра бывает такой сложной,что  средний ум бы с ней   не справился, что делает сам  процесс   игры  с отношениями весьма увлекательным  занятием :)
Пусть Bp=j  Bp/Hp=2z/c=2z/(2z/7)=7
Hp=j/7.
В силу симметрии задачи(на каждой  стороне те же  отношения )
Bp/Bf=7/3
Bf=3j/7
Откуда: fH=j-j/7-3j/7=3j/7
HB=j-j/7=6j/7
BH/fH=6/7*7/3=2  :) 
Осталось еще 1  отношение
MH/Hg но  в целом  из симметрии  выходит  что  по  тем же принципам:  MC=k  Mg=k/7 Hg=3k/7 :)
MH/Hg=4/7 *7/3=4/3
Ну  вот и вся задача осталось поиграть  с площадями. :)
SBMH=4/3*2*S=8/3 S
SBMC=8/3*7/4S=14S/3
SABC=14S/3*3/2=7S
Сошлось :) Я  саму игру площадей не расписывал  если нужно напишу.












.

Answer 3

Для обычного человека возможно вызовет затруднения. Вот так чисто логически поиграть

Answer 4

Но хорошее увлекательное упражнение

Answer 5

Но ваше решение оптимальней тут не поспоришь