Предмет: Алгебра,
автор: Аноним
уравнение 3/х+1/х-1+4/х-2+4/х-3+1/х-4+3/х-5=0
Ответы
Автор ответа:
0
ДОмножаем на x(x-1)(x-2)(x-3)(x-4)(x-5)получаем
Пусть x²-5x = t
Обратная замена
ОТвет:
Автор ответа:
0
◕‿◕◕‿◕** Решение во вложении **.◕‿◕◕‿◕
Приложения:
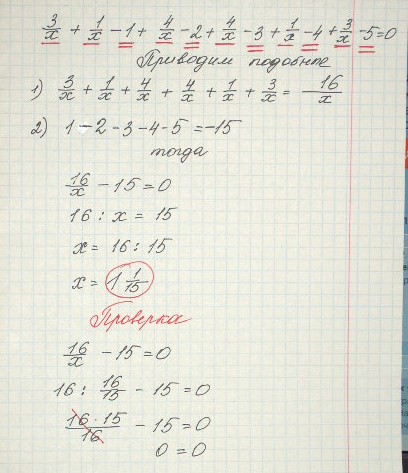
Похожие вопросы
Предмет: Математика,
автор: kiryakazakov0455
Предмет: Математика,
автор: andrushka978
Предмет: История,
автор: alishersartaev659
Предмет: Алгебра,
автор: digitalshadow
Предмет: Математика,
автор: Аноним