Question

Докажите, что биссектриса внешнего угла при вершине, противоположной основанию равнобедренного треугольника, параллельна ему.

Answer 1

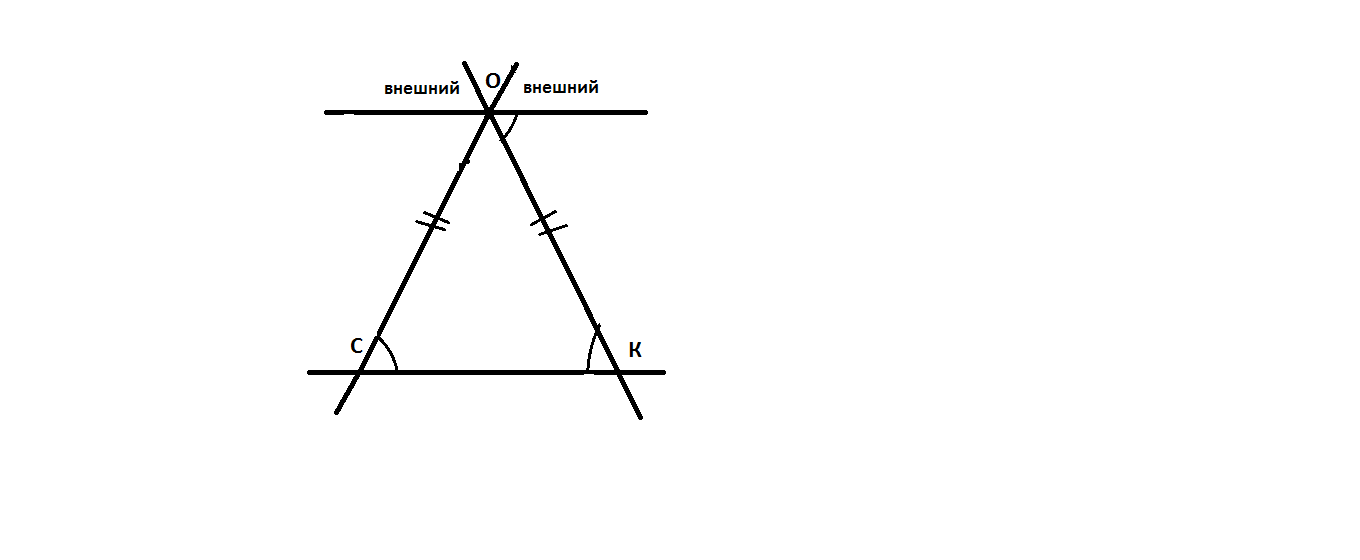
Ок-секущая относительно параллельных пямых. Угол ОКС=ОСК=КОА как накрестлежащие.Но надо еще доказать, что эти прямые параллельные. И это дакажем  равенством этих углов. Т к  внешний угл треугольника равен сумме двух углов треугольника не смежных с ним, и дан равнобедренный треугольник (ОСК=ОКС), то получается что смежный угол равен половине суммы этих углов. А т к они равны, то и угол АОК равен им.