Question

. Треугольник ABC обладает тем свойством, что центры вписанной и описанной окружностей симметричны относительно стороны AC .Найти углы треугольникаABC .

Answer 1

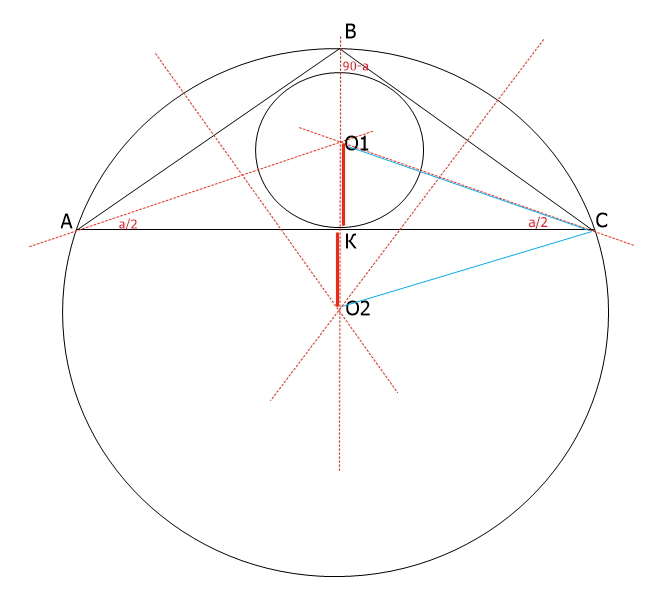
т.к. центры окружностей симметричны --> они лежат на перпендикуляре к АС и на равных расстояниях от АС (О1К = О2К)))
центр вписанной окружности О1 -- это точка пересечения биссектрис, 
центр описанной окружности О2 -- это точка пересечения серединных перпендикуляров... 
следовательно, одна и та же прямая (на которой лежат оба центра окружностей) является и серединным перпендикуляром и биссектрисой, т.е. данный треугольник АВС --- равнобедренный))) 
и два угла при основании равнобедренного треугольника равны... 
обозначим их (а) = ВАС = ВСА
и осталось рассмотреть треугольник ВО2С --- он тоже равнобедренный, т.к. ВО2 = СО2 и его вершина О2 лежит на серединном перпендикуляре))), значит и углы при основании равны...
т.е. угол СВО2 = 90-а = ВСО2 = 3*а/2 
отсюда: 90 = 5*а/2 ---> а = 36
Углы треугольника АВС: 36, 36, 108 градусов

Answer 2

и треугольник СО1О2 получился равнобедренным... СО1 = СО2

Answer 3

значит СК в нем биссектриса, высота и медиана...

Answer 4

т.е. угол ВСО2 состоит из трех одинаковых углов по (а/2)

Answer 5

а т.к. ВО2С равнобедренный, то углы при основании равны...

Answer 6

АКВ --прямоугольный, один острый угол обозначила (а), второй острый угол = 90-а