Предмет: Геометрия,
автор: 4РИМ
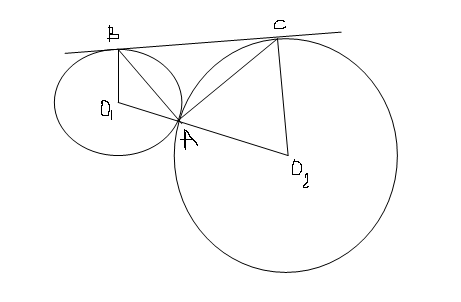
К двум окружностям с центрами в точках О1,О2,касающимся внешним образом в точке А, проведена общая касательная ВС(В и С-точки ксания).Докажите,что угол ВАС-прямой.
Я гиа 2015 готовлюсь летом!)
Ответы
Автор ответа:
0
Треугольник АСО2 и АВО1 равнобедренные, т.к. стороны - радиусы. Значит углы АСО2=САО2, АВО1=ВАО1. Т.к. уголы В и С = 90 касательная к окружности, то из трапеции ВСО1О2 сумма углов О1 и О2 = 180. Из треугольников АСО2 и АВО1: угол АО1В=180-О1ВА*2, АО2С = 180-2*О2СА. их сумма = 180, значит 180=180-О1ВА*2+180-2*О2СА, т.е. О1ВА+О2СА=90. угол ВСА = 90-О2СА, АВС = 90-О1ВА. Т.к. сумма углов треугольника 180 имеем искомый угол = 180-(90-О2СА)-(90-О1ВА) =О1ВА+О2СА, что как уже ранее рассмотрено =90 .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kosobokovatanya
Предмет: География,
автор: yonkada
Предмет: Математика,
автор: bogrussion
Предмет: Биология,
автор: katrinm02
Предмет: Физика,
автор: pepuwer