Question

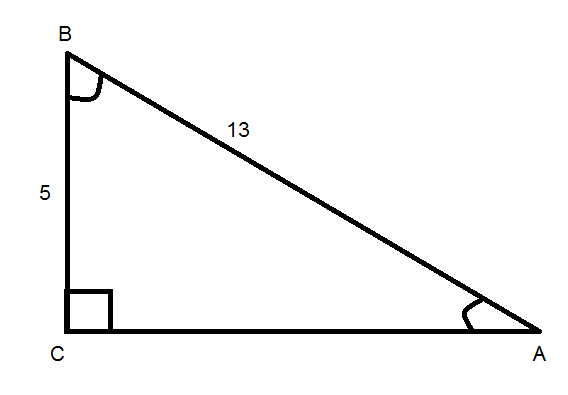
Гипотенуза прямоугольного треугольника равна 13 см, а один из катетов - 5 см.Найдите биссектрису треугольника, проведенную из вершины большего острого угла.

Answer 1

Найдём второй катет =12 см. Так как биссектриса проведена из большего острого угла, то она проведена к 12 см, так чем больше угол, тем больше противолежащая ему сторона. Отношение отрезков, на которые разделила биссектриса катет, будет равно отношению прилежащих к ним гипотенузы и катета => x/(12-x)=5/13=> то есть отрезок, прилежащий к катету(x) и образующий с ним угол 90 градусов равен 10/3, а отсюда по теореме Пифагора найдём и биссектрису = корню из (100/9+25) 

Answer 2

Рисунок вам дан.
Определим второй катет по т.Пифагора
$b= sqrt{c^2-a^2}= sqrt{13^2-5^2} =12$
Определим какой угол больший
tg А = AC/BC - отношение противолежащего катета к прилежащему катету
tg А = 5/12;
$A=arctg( frac{5}{12} )=22.65а$
Значит, угол В = 90-22,65=67,38 - наибольший
Наидем биссектрису угла В
$b_B= frac{ sqrt{a*c(b+a+c)(a+c-b)} }{a+c} = frac{ sqrt{5*13(13+5+12)(5+13-12)} }{5+13}= frac{5 sqrt{13} }{3}$