Предмет: Алгебра,
автор: pak0498
Помогите решить уравнение, пожалуйста...
Приложения:
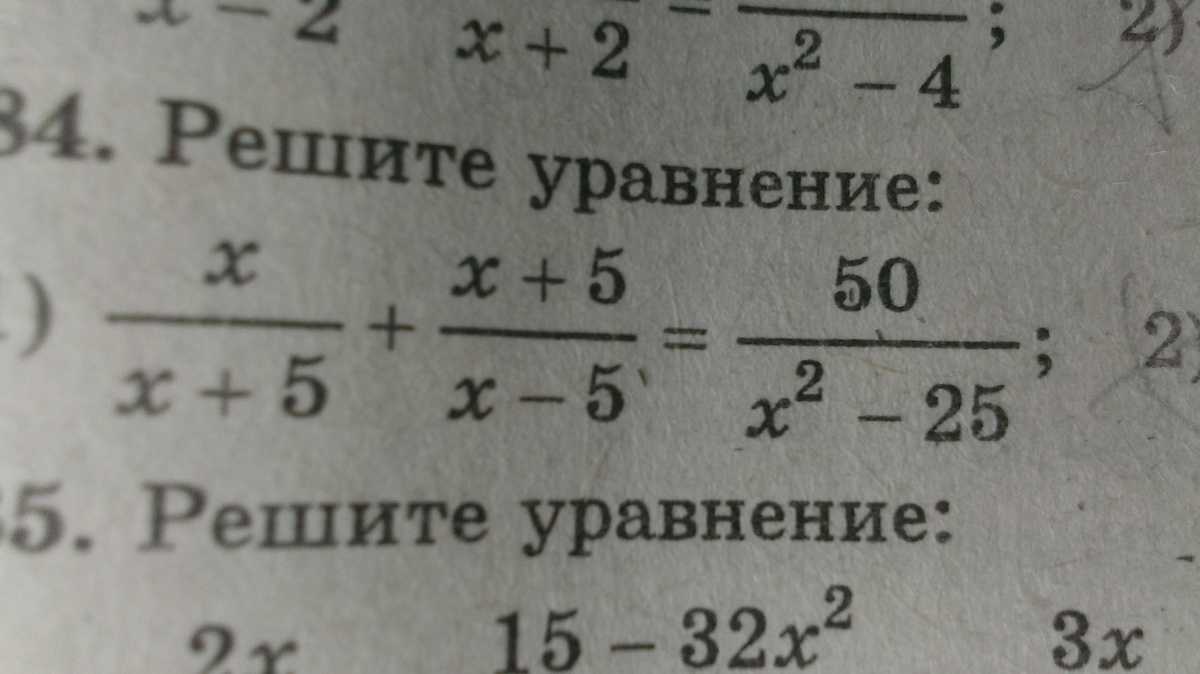
Ответы
Автор ответа:
0
две дроби равны, когда числитель и знаменатель равны:
последний корень не удовлетворяет области определения,
поэтому корень будет только 2,5
Похожие вопросы
Предмет: Литература,
автор: AMuslima58
Предмет: Немецкий язык,
автор: Аноним
Предмет: Алгебра,
автор: elistratovad5
Предмет: Математика,
автор: dmb7927
Предмет: Математика,
автор: Skulelena85