Предмет: Математика,
автор: tashakalinger
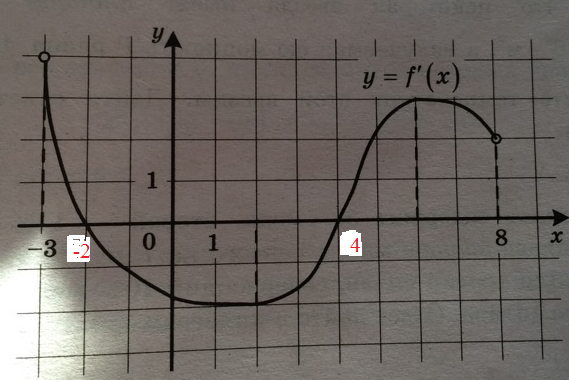
На рисунке изображен график функции y=f(x) - производной функции f(x), определенной на интервале (-3;8). Найдите точку минимума функции f(x).
Приложения:

Ответы
Автор ответа:
0
Необходимое условие экстремума: производная равна нулю.
Производная данной функции обращается в ноль в точках -2 и 4
Эти точки являются точками возможных экстремумов. Чтобы узнать есть в каждой из этих точек экстремум надо воспользоваться теоремой- достаточное условие экстремума функции.
х₀- точка, в которой производная равна нулю. Если при переходе через точку х₀ производная меняет знак с "+" на "-", то х₀- точка максимума, если с "-" на "+", то точка минимума.
При переходе через точку х=4 производная меняет знак с "-" на "+"
График расположен ниже оси ох, а после точки 4 выше оси ох.
х=4 - точка минимума
Производная данной функции обращается в ноль в точках -2 и 4
Эти точки являются точками возможных экстремумов. Чтобы узнать есть в каждой из этих точек экстремум надо воспользоваться теоремой- достаточное условие экстремума функции.
х₀- точка, в которой производная равна нулю. Если при переходе через точку х₀ производная меняет знак с "+" на "-", то х₀- точка максимума, если с "-" на "+", то точка минимума.
При переходе через точку х=4 производная меняет знак с "-" на "+"
График расположен ниже оси ох, а после точки 4 выше оси ох.
х=4 - точка минимума
Приложения:
Автор ответа:
0
...................................
Приложения:

Похожие вопросы
Предмет: Обществознание,
автор: Venaithell
Предмет: Информатика,
автор: Asylzhanmmmmmmm
Предмет: Қазақ тiлi,
автор: alikkapparuly
Предмет: Математика,
автор: 2002natella