Предмет: Алгебра,
автор: Elverd
Помогите пожалуйсто решить
Приложения:

Ответы
Автор ответа:
0
Воспользуемся свойством степеней
Пусть
Производим группировку
Нет решений
Ответ: 0,5
Второе уравнение во вложение
3. ОДЗ
Воспользуемся формулами перехода к новому основанию логарифма
Переворачиваем дробь
Воспользуемся свойством логарифмов
Раскрываем скобки
Находим дискриминант
Дискриминант положителен значит уравнение имеет 2 корня
Ответ:
Приложения:
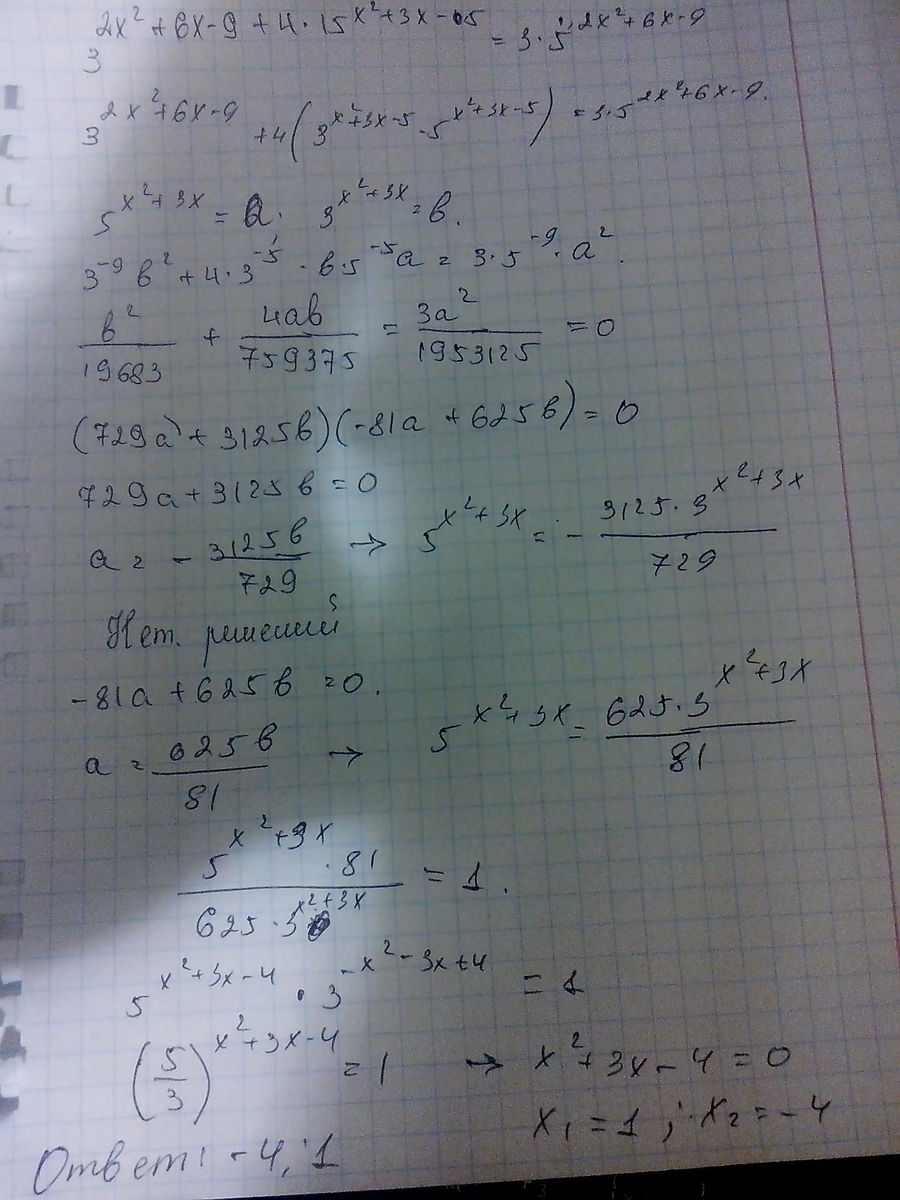
Автор ответа:
0
......................................................
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: mirzayevafarida2006
Предмет: Физика,
автор: Popkovvn577
Предмет: География,
автор: AngryCloud99
Предмет: История,
автор: raufka99