Question

 Треугольник ABC, стороны которого 13 см, 14 см и 15 см, разбит на три
треугольника отрезками, соединяющими точку пересечения медиан M с вершинами треугольника. Найдите площадь
треугольника BMC?

Answer 1

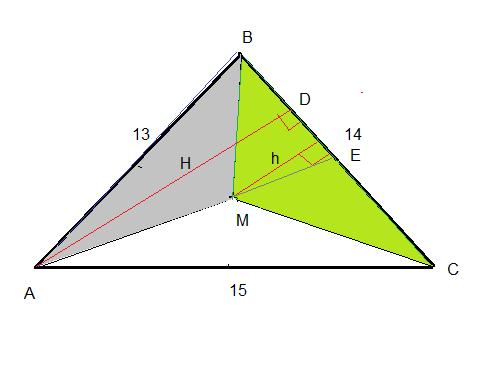
Площадь треугольника АВС вычислим по формуле Герона.
р=(13+14+15)/2=21
$S= sqrt{p(p-a)(p-b)(p-c)} = sqrt{21(21-13)(21-14)(21-15)}= \ =sqrt{21cdot 8cdot 7cdot 6}=7cdot 12=84$

С другой стороны площадь треугольника равна половине произведения  основания на высоту. Пусть ВС основание, высота АD=H
ВС·H/2=84⇒ 14·H=168,  значит H=12
Проведем h=MK треугольника ВМС. Основание ВС=14.

Чтобы найти h =MK  рассмотрим треугольник АDE, АЕ- медиана к стороне ВС. Медиана в точке М-точке пересечения медиан -делится в отношении 2:1, считая от вершины. Значит  АМ:МЕ=2:1, а  АЕ:МЕ=3:1

Δ МКЕ подобен Δ ADE:
АЕ:МЕ=AD:MK  ⇒ 
H=3h
h=H/3=12/3=4
S(ΔBMC)=14·4/2=28

Высота треугольника ВМС в три раза меньше высоты АD треугольника АВС.
Значит и площадь этого треугольника в три раза меньше.
 S(ΔВМС)=1/3 S(ΔABC)=84/3=28 кв см.

Между прочим и площади двух других треугольников тоже 28 кв. см