Question

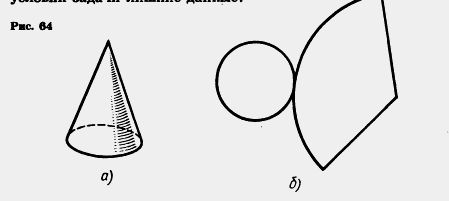
 На рисунке 64, а изображен конус. Основание конуса — круг, а развертка боковой поверхности — сектор (см. рис. 64, б). Вычислите площадь поверхности конуса, если радиус еТо основания 3 см, а развертка боковой поверхности — сектор с прямым углом, радиус этого сектора 12 см. Есть ли в условии задачи лишние данные?

Answer 1

Площадь полной поверхности конуса равна сумме площадей основания конуса и его боковой поверхности.
S=πrl+πr², где l - образующая конуса, r - радиус основания
l=12см
r=3cм
S=12*3π+3²π=45π=45*3,14≈141(см²)
Лишнее в условии - прямой угол.