Предмет: Геометрия,
автор: Markus755
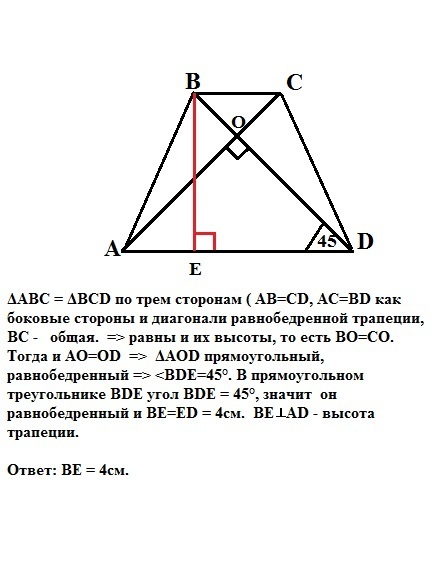
В равнобедренной трапеции ABCD ( AD и BC -основания) диагонали взаимно перпендикулярны. BE перпенд. АD; ED= 4см.
чему равна высота трапеции?
Ответы
Автор ответа:
0
ΔАВС = ΔВСD по трем сторонам ( АВ=CD, AC=BD как боковые стороны и диагонали равнобедренной трапеции, ВС - общая. => равны и их высоты, то есть ВО=СО. Тогда и АО=OD => ΔAOD прямоугольный, равнобедренный => <BDE=45°. В прямоугольном треугольнике BDE угол BDE = 45°, значит он равнобедренный и ВЕ=ED = 4см. ВЕ⊥AD - высота трапеции.
Ответ: ВЕ = 4см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська література,
автор: voronglaz54
Предмет: Математика,
автор: sadykovaarina
Предмет: Математика,
автор: irina721