Предмет: Алгебра,
автор: utopia
Найдите область определения функции
y=
Ответы
Автор ответа:
0
Определим нули функции
Находим дискриминант
Дискриминант положителен, значит уравнение имеет 2 корня
Воспользуемся формулой корней квадратного уравнения
Определим нули функции
Находим дискриминант
Дискриминант положителен, значит уравнение имеет 2 корня
Воспользуемся формулой корней квадратного уравнения
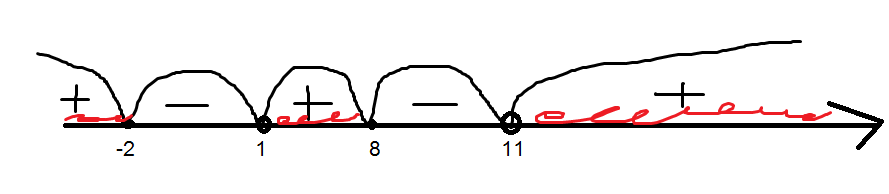
Знаки на промежутке смотреть во вложения
Ответ:
Приложения:
Автор ответа:
0
да,потерян промежуток
Автор ответа:
0
как так потерял((
Похожие вопросы
Предмет: Биология,
автор: Ychenikvov
Предмет: Математика,
автор: andreikostya2008
Предмет: Алгебра,
автор: zenuy56
Предмет: Физика,
автор: viktorostoyach