Предмет: Геометрия,
автор: 11z11
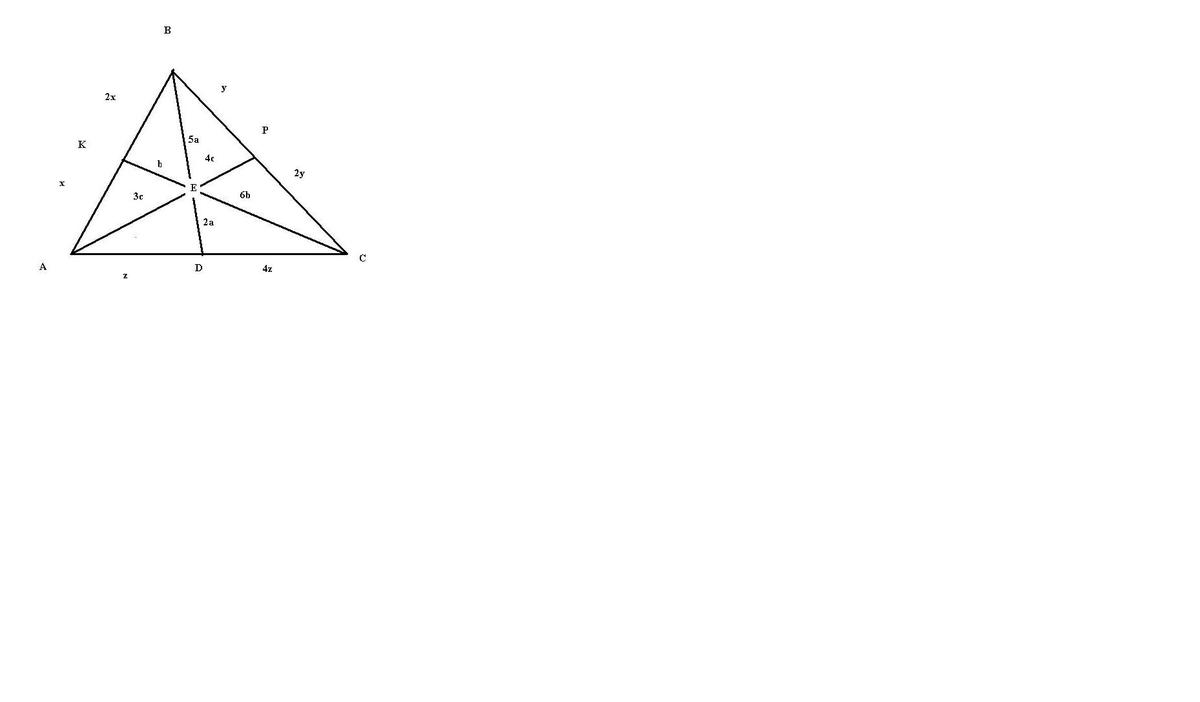
В треугольнике ABC на сторонах AB и BC взяты соответственно точки К и P так, что AK : KB = 1 : 2, CP : PB = 2 : 1. Прямые AP и CK пересекаются в точке E. Найдите площадь треугольника ABC, если площадь треугольника BEC равна 4.
Ответы
Автор ответа:
0
Опустим прямую  так чтобы она пересекала точку
так чтобы она пересекала точку  , по теорема Ван Обеля и Чевы соответственно получаем
, по теорема Ван Обеля и Чевы соответственно получаем



ответ
Есть более короткое решение по теореме МЕНЕЛАЯ
 , тогда площадь треугольника
, тогда площадь треугольника

ответ
Есть более короткое решение по теореме МЕНЕЛАЯ
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: brilliant1014
Предмет: Физика,
автор: karinakit2010
Предмет: Физика,
автор: Werboys
Предмет: Алгебра,
автор: yana9611