Предмет: Алгебра,
автор: абитурьент
найти наибольшее целое решение неравенства (5-x)*(x^2-6x+5)/(x^3-25) больше или равно 0
Ответы
Автор ответа:
0
1. Рассмотрим функцию и определим область определения функции
![y= frac{(5-x)(x^2-6x+5)}{x^3-25} \ x^3-25 neq 0 \ x neq sqrt[3]{25} \ D(y)=(-infty;sqrt[3]{25})U(sqrt[3]{25};+infty) y= frac{(5-x)(x^2-6x+5)}{x^3-25} \ x^3-25 neq 0 \ x neq sqrt[3]{25} \ D(y)=(-infty;sqrt[3]{25})U(sqrt[3]{25};+infty)](https://tex.z-dn.net/?f=y%3D+frac%7B%285-x%29%28x%5E2-6x%2B5%29%7D%7Bx%5E3-25%7D++%5C+x%5E3-25+neq+0+%5C+x+neq++sqrt%5B3%5D%7B25%7D++%5C+D%28y%29%3D%28-infty%3Bsqrt%5B3%5D%7B25%7D%29U%28sqrt%5B3%5D%7B25%7D%3B%2Binfty%29)
1.Определим нули функции

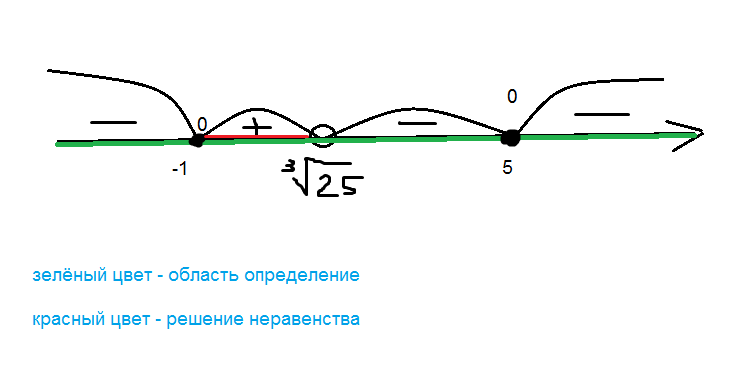
3. Знаки на промежутке (смотреть во вложения)
Решение неравенства - [1;∛25) U {5}
Наибольшее целое будет 5
Ответ: 5.
1.Определим нули функции
3. Знаки на промежутке (смотреть во вложения)
Решение неравенства - [1;∛25) U {5}
Наибольшее целое будет 5
Ответ: 5.
Приложения:
Автор ответа:
0
андрей, точка то 1, а не -1)) а так все правильно)
Автор ответа:
0
если конечно условие записано верно)
Автор ответа:
0
//////////////////////////////////////////////////////////////////////////
Приложения:

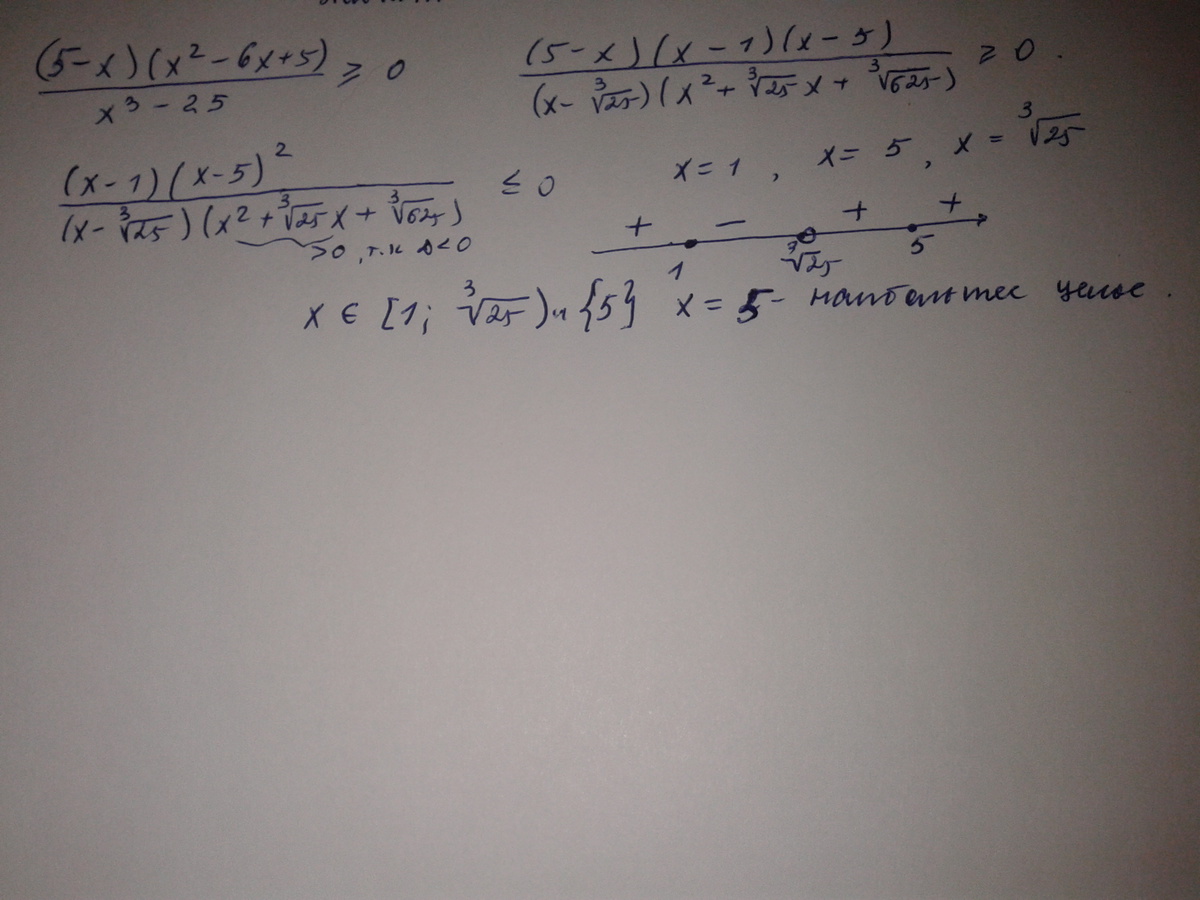
Похожие вопросы
Предмет: Другие предметы,
автор: I450
Предмет: Физика,
автор: andriytkachenko08
Предмет: Геометрия,
автор: nonamebro04
Предмет: Экономика,
автор: Dashunka2000
Предмет: История,
автор: vaskatyaui