Question

Здравствуйте! Помогите пожалуйста решить задание. 1. В равнобокой трапеции большее основание равно 16 см., боковая сторона 2 корень квадратный из 3 см., угол при основании 30 градусов. Меньше основание трапеции равно? 
2. Диагонали трех граней прямоугольного параллелепипида, сходящиеся в одной вершине, равны 5, 6, 7. Линейные размеры параллелепипида равны?
Если можно с решением пожалуйста! Заранее спасибо!

Answer 1

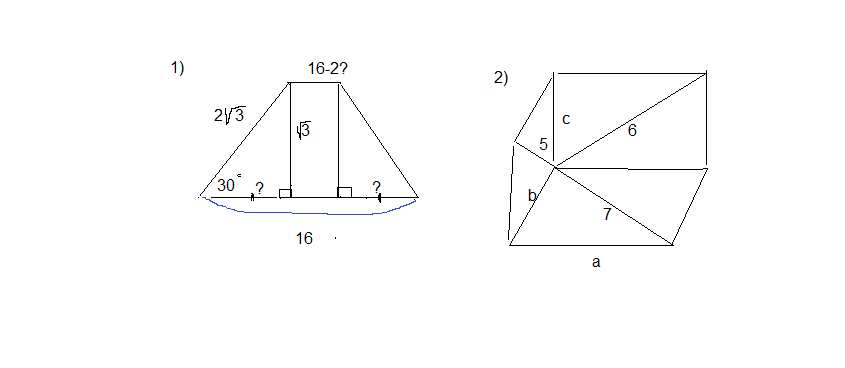
1) Проведем высоты из вершин верхнего основания на нижнее.( см. рисунок)
     Из прямоугольного треугольника с углом в 30⁰ высота трапеции - катет, лежащий против угла в 30⁰, и потому высота равна половине гипотенузы или √3
Второй катет, находим по теореме Пифагора
(2√3)²-(√3)²=12-3=9
Катет равен 3,отмечен на рисунке(?) Два таких катета на нижнем основании
 равны, значит верхнее основание 16-2·?=16-6=10
  ответ. верхнее основание равно 10 см.
2) см. рисунок. Параллелепипед в незавершенном виде, но хорошо видны плоскости основания, и двух боковых граней и три диагонали, сходящиеся в одной вершине.
Обозначим линейные размеры параллелепипеда  a, b, c
По теореме Пифагора:
a²+b²=7²
b²+c²=5²
a²+c²=6²
 Сложим три уравнения:
2a²+2b²+2c²=49+25+36, тогда
а²+b²+c²=55
заменим a²+b²=49, тогда 49+с²=55    ⇒    с²=6, с=√6
заменим b²+c²=25,  тогда а²+25=55   ⇒  а²=30, а=√30
заменим а²+с²=36, тогда b²+36=55    ⇒  b²=19, b=√19
Ответ. линейные размеры параллелепипеда  √30, √19,  √6.

Answer 2

Рада, что помогла!