Question

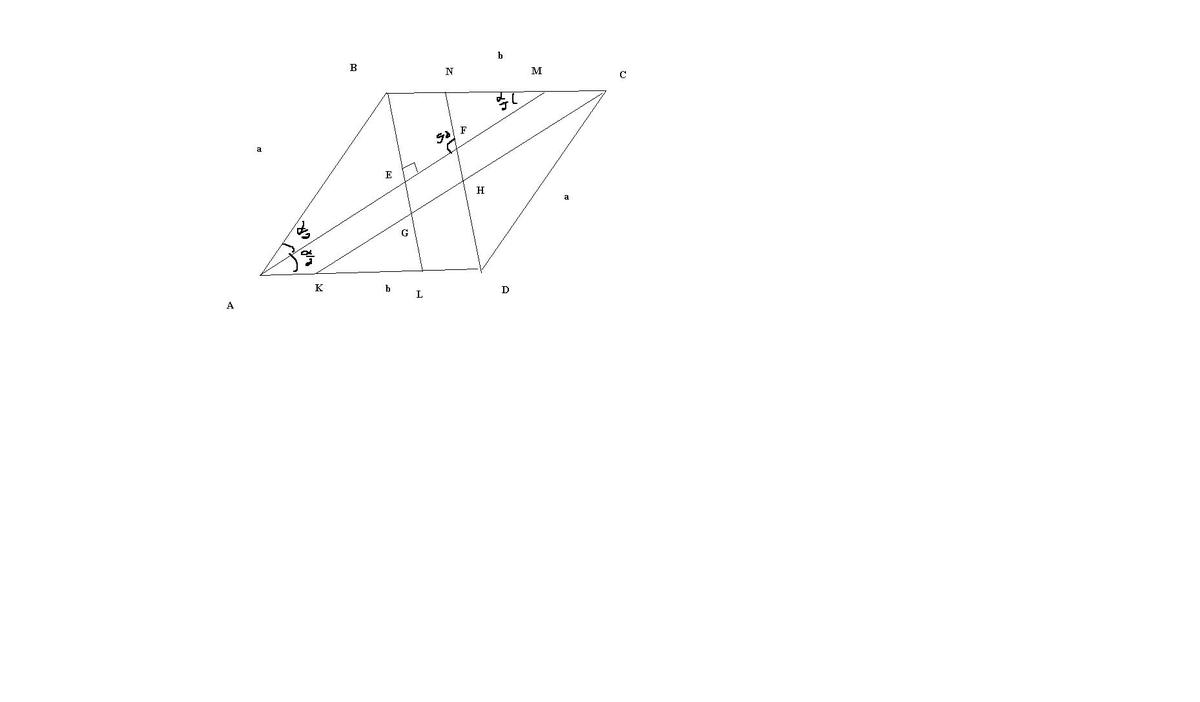
Со сторонами а и b и углом a проведены биссектрисы четырех углов. Найти площадь четырехугольника, ограниченного биссектрисами.

Answer 1

 Положим что четырехугольник $EFGH$ образовался , при пересечений всех биссектрис . 
Положим что угол    $BAD= alpha$ , то угол $CDA=180- alpha$ 
$BEA=90а$  как и все углы . 
Треугольник$BEA$   прямоугольный . 
 $AB=a\ AD=b\\ BE=a*sinfrac{ alpha }{2}$ 
 $GL=(2a-b)sinfrac{ alpha }{2}\ BL=sqrt{2a^2-2a^2*cos alpha}=asqrt{2(1-cosa)}\ EG=a*2sinfrac{a}{2}-(2a-b)sinfrac{a}{2}-a*sinfrac{a}{2} = (b-a)sinfrac{a}{2}$ 
 $FM=(2a-b)cosfrac{a}{2}\ AE=a*cosfrac{a}{2} \ EF=sqrt{2a^2+2a^2cosa}-a*cosfrac{a}{2}-(2a-b)cosfrac{a}{2} =(b-a)cosfrac{a}{2} \  S=(b-a)^2*sinfrac{a}{2}*cosfrac{a}{2}=(b-a)^2*sina*0.5$  
        
 $S_{EFGH}=(b-a)^2sina*0.5$
  

Answer 2

Там очевидно сторону строим паралельную и через синус

Answer 3

рад

Answer 4

Я на самом деле уже давно решил. Пытался рисунок нарисовать. Но потом лениво стало и передумал