Question

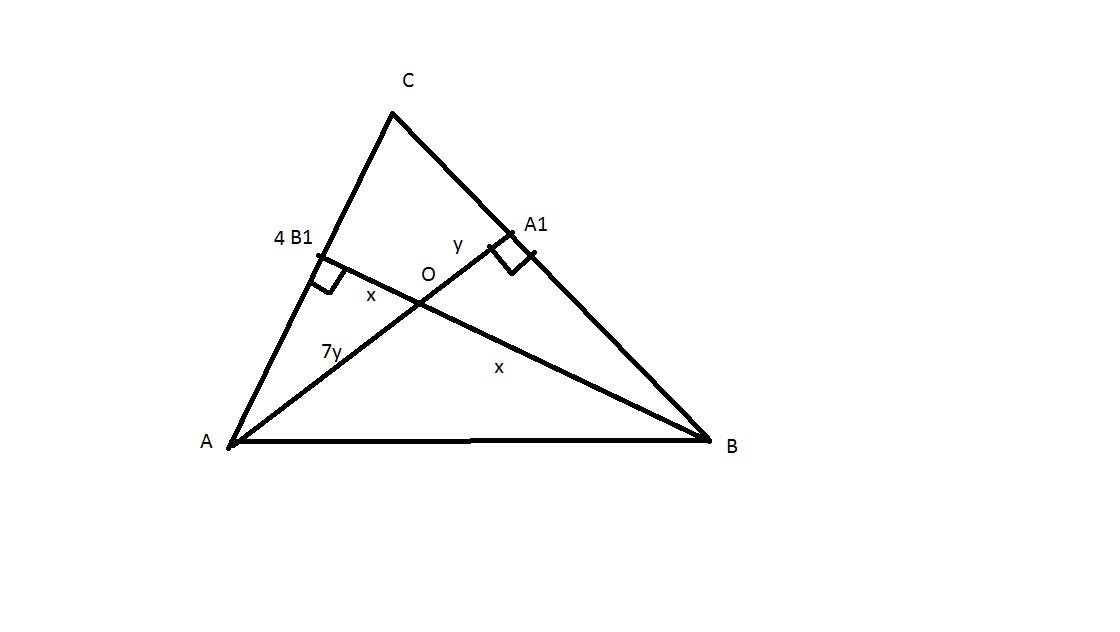
В треугольнике ABC высоты AA₁ и BB₁ пересекаются в точке O. Известно, что BO=OB₁, AO:OA₁=7, AC=4. Найти AB, BC и A₁B₁.

Answer 1

Обозначим  для удобства доли отношений:
OA=7y
OA1=y
BO=OB1=x
Из подобия прямоугольных треугольников  по острому углу AOB1 и A1OB
Получим   y/x=x/7y
x^2=7y^2
x=√7y
Площадь треугольника   можно найти 2   способами:
SABC=1/2*2x*4=1/2*8y*BC
8x=8y*BC
x=y*BC
√7y=y*BC
BC=√7
Рассмотрим прямоугольный  треугольник   треугольник AB1O
sin OAB1=x/7y=√7y/7y=1/√7
Откуда  тк   C=90-OAB1  то  cosC=cos(90-OAB1)=sinOAB1=1/√7
Теперь по  теореме  косинусов  найдем 3  сторону:
AB^2=16+7-2*4*√7*1/√7=16+7-8=15
AB=√15
Рассмотрим  прямоугольные треугольники  CAA1 и   CBB1
Из  них получим: СB1=CB*cosС=√7*1/√7=1
CA1=AC*cosC=4/√7
И  наконец 2 раз применим теорему косинусов:

A1B1^2=1+16/7-2*1*4/√7*1/√7=1+16/7-8/7=1+8/7=15/7
A1B1=√15/7
Ответ:BC=√7  AB=√15 A1B1=√15/7

Answer 2

При многом благодарен за решение. А второй раз задал эту задачу, т.к. думал, что ее удалили, виноват