Question

прямая , параллельная основаниям трапеции АВСD, пересекает ее боковые стороныАВ и СD в точках Е и F соответственно. найдите длину отрезка EF , если АD= 42, BC=14, CF: DF=4:3

Answer 1

трапеция АВСD, ВС=14, АD=42,
СF/DF=4/3=4х/3х,
СF+DF=3х+4х=7х,
Проведем ВН параллельную СD, получается НВСD - паралелограмм, ВН и ЕF пересекаются в точке O. 
ВС=OF=НD=14,
ВН=СD=7х,
ВO=СF=4х,
АН=АD-НD=42-14=28,
Δ АВН подобен Δ ЕВO по двум равным углам (угол АВН - общий, угол АНВ = угол ЕOВ как соответственный),
ВO/ВН=ЕO/АН,
4х/7х=ЕO/28,
ЕO=4х*28/7х=16,
ЕF=ЕO+OF=16+14=30

Answer 2

Вариант решения.
В данной трапеции ВЕ:ЕА  равно 4:3 ( по  теореме Фалеса параллельные прямые отсекают на секущих прямых пропорциональные отрезки),
причем  трапеция диагональю BD и прямой EF поделена на подобные треугольники:
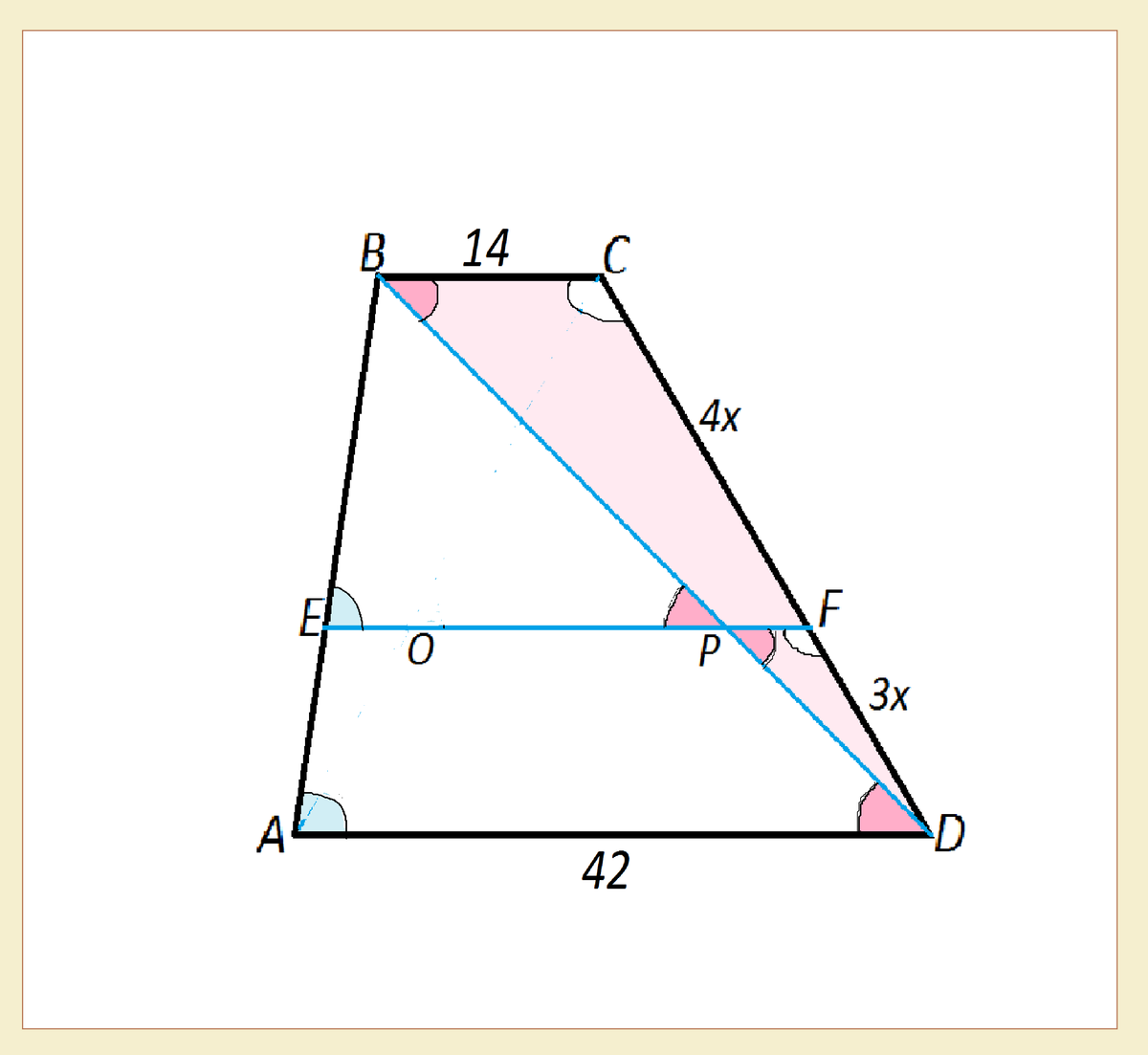
 ∆ BCD ~ ∆ PFD и
△ BAD ~ △ BEP, так как  углы при основаниях этих треугольников равны как углы при параллельных прямых и секущей, а углы при вершинах - общие (см. рисунок). 
Пусть коэффициент отношения отрезков боковой стороны СD равен х.
Тогда в ∆ BCD  и ∆ PFD 
CD=7x
CD:FD=BC:PF
7х:3х=14:PF
PF=42:7=6 cм
В ∆ BAD и ∆ BEP пусть коэффициент отношения отрезков АВ равен у
ВА:ВЕ=42:EP 
7у:4у=42:EP 
4*42=7 EP
EP=4*6=24
EF=EP+PE=24+6=30 (единиц длины)