Question

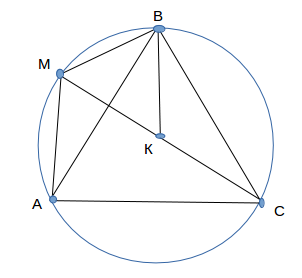
Правильный треугольник АВС вписан круг. Доказать, что расстояние от произвольной точки М на этом круге к одной вершин треугольника равен сумме расстояний до двух других его вершин

Answer 1

Пусть точка М лежит на дуге АВ. Возьмём на МС точку К, так чтоб МК = МВ. Поскольку дуга ВС = 120°, то ∠BMC =60°. Следовательно, ΔМBK — равносторонний. Тогда ∠МВА =∠МВК-∠АВК=60° -∠АВК=∠АВС-∠АВК=∠КВС. Поэтому ΔМВА = ΔКВС (потому что МВ = ВК, АВ = ВС, ∠ВМА=∠КВС). Отсюда следует, что МА+МВ=ВК+СК=МК+СК=МС. Что и требовалось доказать.