Question

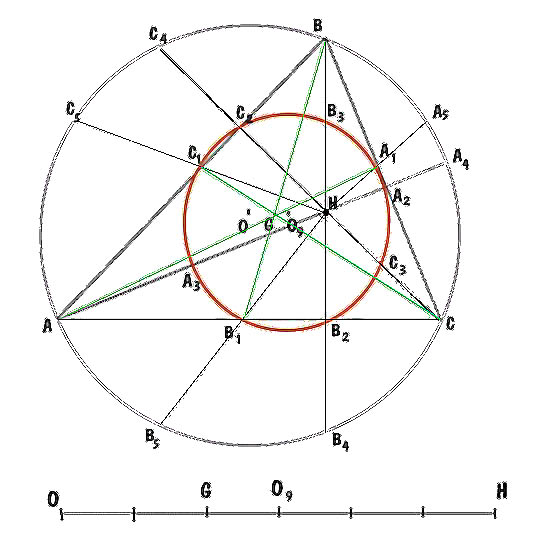
Доказать, что середины сторон треугольника, основания высот и середины отрезков, соединяющих точку Н пересечения высот с вершинами треугольника, лежат на одной окружности, причем центр Р круга с серединой ОН, где О - центр окружности, описанной вокруг заданного треугольника АВС.

Answer 1

Пусть A1,B1 и C1- середины сторон BC,CA и AB;
 A2,B2 и C2- основания высот;  
A3,B3 и C3- середины отрезков, соединяющих точку пересечения высот с вершинами.
Так как A2C1 = C1A = A1B1 и A1A2||B1C1, точка A2 лежит на описанной окружности треугольника A1B1C1.
 Аналогично точки B2 и C2 лежат на описанной окружности треугольника A1B1C1.
Рассмотрим теперь окружность S с диаметром A1A3. Так как A1B3||CC2 и A3B3||AB, то <A1B3A3 = 90°, а значит, точка B3 лежит на окружности S.
Аналогично доказывается, что точки C1,B1 и C3 лежат на окружности S. Окружность S проходит через вершины треугольника A1B1C1, поэтому она является его описанной окружностью.
При гомотетии с центром H и коэффициентом 1/2 описанная окружность треугольника ABC переходит в описанную окружность треугольника A3B3C3, т. е. в окружность девяти точек. Значит, при этой гомотетии точка O переходит в центр окружности девяти точек.