Предмет: Геометрия,
автор: Frag32
Доведіть, що довільна площина, яка проходить через середи двох мимобіжних ребе тетраедра, ділить його об'єм навпіл
Русский_
Докажите, что произвольное плоскость, проходящая через середины двух скрещивающихся ребе тетраэдра, делит его объем пополам
Ответы
Автор ответа:
0
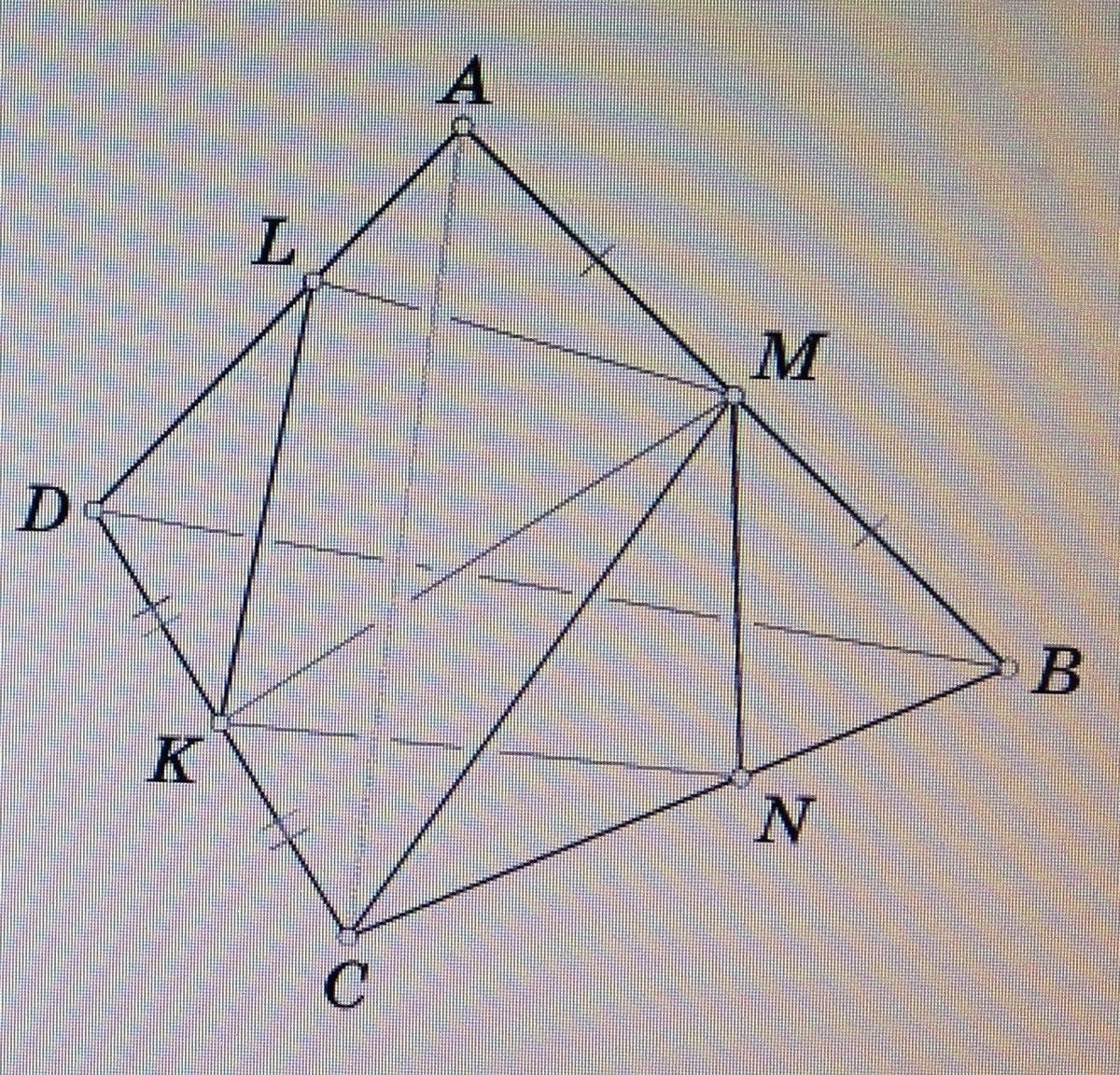
Пусть М и К - середины ребер АВ и СD тетраэдра ABCD.
Пусть плоскость, проходящая через М и К, пересекает ребра АD и ВС в точках L и N.
Плоскость DMC делит тетраэдр на 2 части равного объема, поэтому достаточно проверить, что равны объемы тетраэдров DKLM и CKNM.
Объем тетраэдра СКВМ равен 1/4 объема тетраэдра ABCD, а отношение объемов тетраэдров СКВМ и CKNM равно ВС:СN. Аналогично отношение 1/4 объема тетраэдра ABCD к объему тетраэдра DKLM равно AD:DL.
ВС:СN=AD:DL
Пусть плоскость, проходящая через М и К, пересекает ребра АD и ВС в точках L и N.
Плоскость DMC делит тетраэдр на 2 части равного объема, поэтому достаточно проверить, что равны объемы тетраэдров DKLM и CKNM.
Объем тетраэдра СКВМ равен 1/4 объема тетраэдра ABCD, а отношение объемов тетраэдров СКВМ и CKNM равно ВС:СN. Аналогично отношение 1/4 объема тетраэдра ABCD к объему тетраэдра DKLM равно AD:DL.
ВС:СN=AD:DL
Приложения:
Автор ответа:
0
браво)))
Автор ответа:
0
спасибо
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Алгебра,
автор: murlomurlovno
Предмет: Математика,
автор: jdjdjjrjdjdjd
Предмет: Химия,
автор: sasharus2013