Question

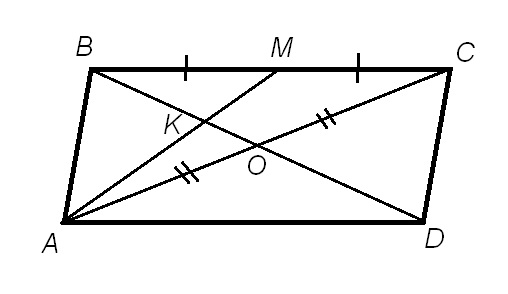
 В параллелограмме ABCD отмечена точка М – середина отрезка ВС. Отрезок АМ пересекается с диагональю BD в точке К. Докажите, что ВК:BD=1:3

Answer 1

Чертеж- во вложении.
Проведем еще диагональ АС. По свойству параллелограмма точка пересечения его диагоналей О - середина каждой из диагоналей.
Значит, К - точка пересечения медиан  ∆АВС. Тогда верно соотношение: ВК:КО=2:1. Т.к. ВО=OD, то ВК=$frac{2}{3}$ВО или ОК=$frac{1}{3}$ВО. Отсюда BD=2BO=2·3OK=6·$frac{1}{2}$BK=3BK.
Наконец, ВК:BD=1:3. Доказано.