Предмет: Алгебра,
автор: Аноним
Уравнение с параметром. Найти все значения параметра b, при которых ровно один корень уравнения (1) удовлетворяет условию (2). Найти этот корнень. Я дошла до 4b^2+4b-1=0, отсюда и нашла b. Что дальше? Как применить условие?
Приложения:
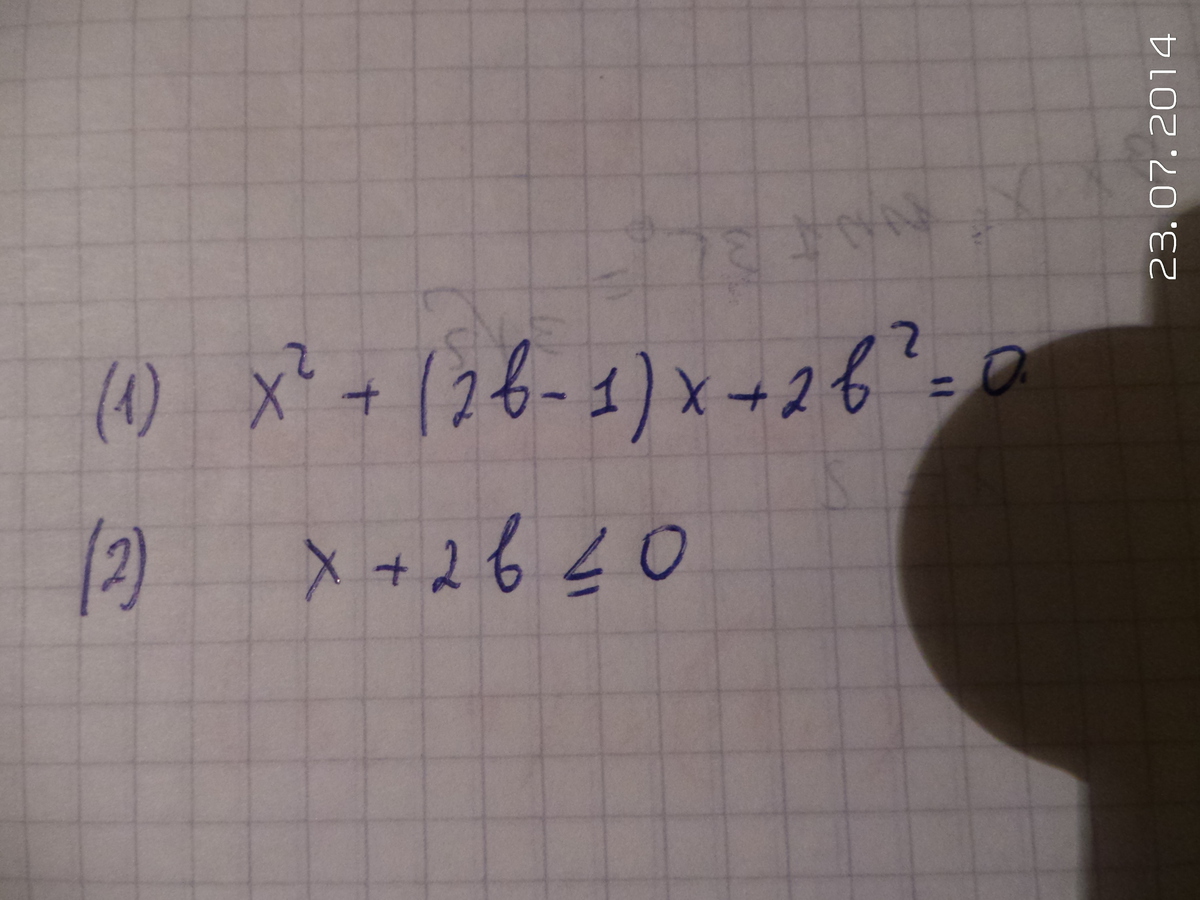
Ответы
Автор ответа:
0
Для упрощения сделаем замену:
t=x+2b откуда t<=0
x=t-2b
(t-2b)^2+(2b-1)(t-2b)+2b^2=0
t^2-4bt+4b^2+2bt-4b^2-t+2b+2b^2=0
t^2-t(2b+1)+2b+2b^2=0
Тк ровно для одного корня выполняется условие
x+2b<=0 t<=0
То очевидно из теоремы виета возможно 2 варианта:
1)D>0
2b+2b^2<=0 тк ( 1 корень положительный или равен 0 ,а другой отрицательный,откуда произведение корней отрицательно) Замечание: когда 2b+2b^2=0 b=0 b=-1 Необходимо проверить что другой корень кроме 0 не отрицательный,если это так ,то это b нужно исключить из множества решений.
2)D=0
t<=0 (Для этого случае просто посмотреть подходит ли корень)
Дальше думаю сами досчитаете
t=x+2b откуда t<=0
x=t-2b
(t-2b)^2+(2b-1)(t-2b)+2b^2=0
t^2-4bt+4b^2+2bt-4b^2-t+2b+2b^2=0
t^2-t(2b+1)+2b+2b^2=0
Тк ровно для одного корня выполняется условие
x+2b<=0 t<=0
То очевидно из теоремы виета возможно 2 варианта:
1)D>0
2b+2b^2<=0 тк ( 1 корень положительный или равен 0 ,а другой отрицательный,откуда произведение корней отрицательно) Замечание: когда 2b+2b^2=0 b=0 b=-1 Необходимо проверить что другой корень кроме 0 не отрицательный,если это так ,то это b нужно исключить из множества решений.
2)D=0
t<=0 (Для этого случае просто посмотреть подходит ли корень)
Дальше думаю сами досчитаете
Автор ответа:
0
Замена это прием позволяющий сравнивать корень с 0,чтобы используя свойство знаков использовать теорему виета
Автор ответа:
0
Есть и другой способ решения. Теоремы о критериях корней. Или для совсем эстетов графическое решение,что требует знание производной и пределов
Автор ответа:
0
Есть еще 1 графический способ в народе его называют (динамика). Но динамику понимают не всt
Автор ответа:
0
Динамика краcивое и эстетичное решение,сводящее его к чистой геометрии. Когда параболы и прямые начинают правать по декартовой системе координат :)
Похожие вопросы