Question

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все ребра которой равны 1, найдите расстояние от точки A до прямой B1C1.

Answer 1

Расстояние от точки до прямой - отрезок от этой точки до прямой, проведенный к ней перпендикулярно. 
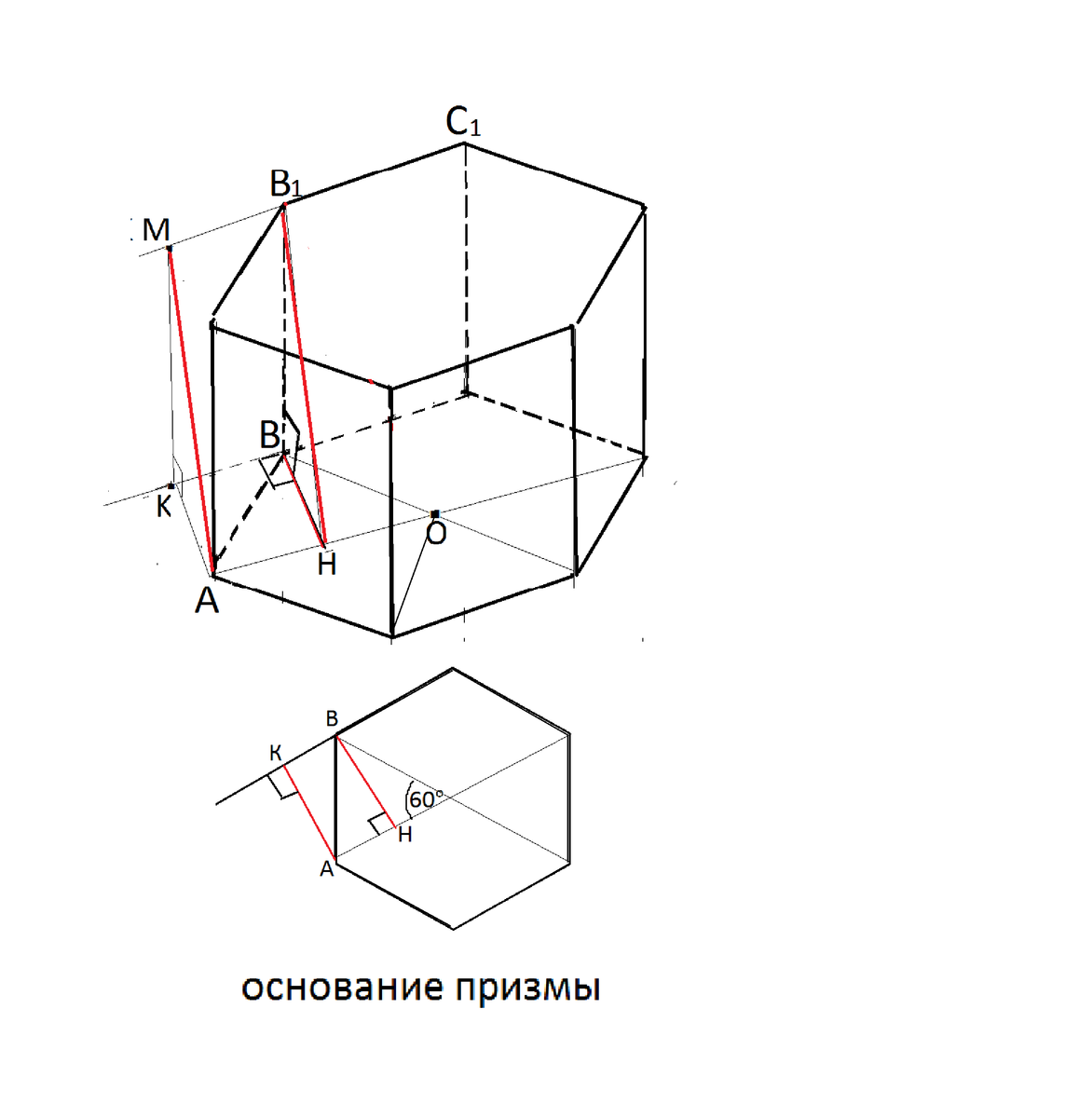
На рисунке в приложении это отрезок АМ.
АМ-наклонная, ее проекция перпендикулярна прямой ВК,
МК - параллельна ВВ1 и перпендикулярна ВК. 
Все ребра призмы равны 1, а её  основание состоит из равносторонних
треугольников. 
Треугольник НВВ1 равен треугольнику АКМ по двум катетам. 
Для удобства перенесём АМ внутрь призмы в параллельную ей В1Н. 
Основания правильной шестиугольной призмы - правильные шестиугольники. АВ=ВО=АО=1. 
В1Н=АМ и является гипотенузой прямоугольного треугольника НВВ1. 
ВН и ВВ1 - катеты, НВ1 - гипотенуза и равна искомому расстоянию АМ. 
ВН- высота равностороннего треугольника со стороной 1. 
ВН=АВ*sin(60°)=(√3):2
НВ1=√(ВН²+ ВВ1² =(√7):2
АМ=НВ1=(√7):2