Question

можно ли расставить на ребрах куба 12 последовательных натуральных чисел так, чтобы суммы на тройках ребер, выходящих из одной вершины были одинаковы?
Помогтте плиз

Answer 1

Сумма  всех 12   чисел равна 4S,где S-сумма   чисел при 1  вершине.
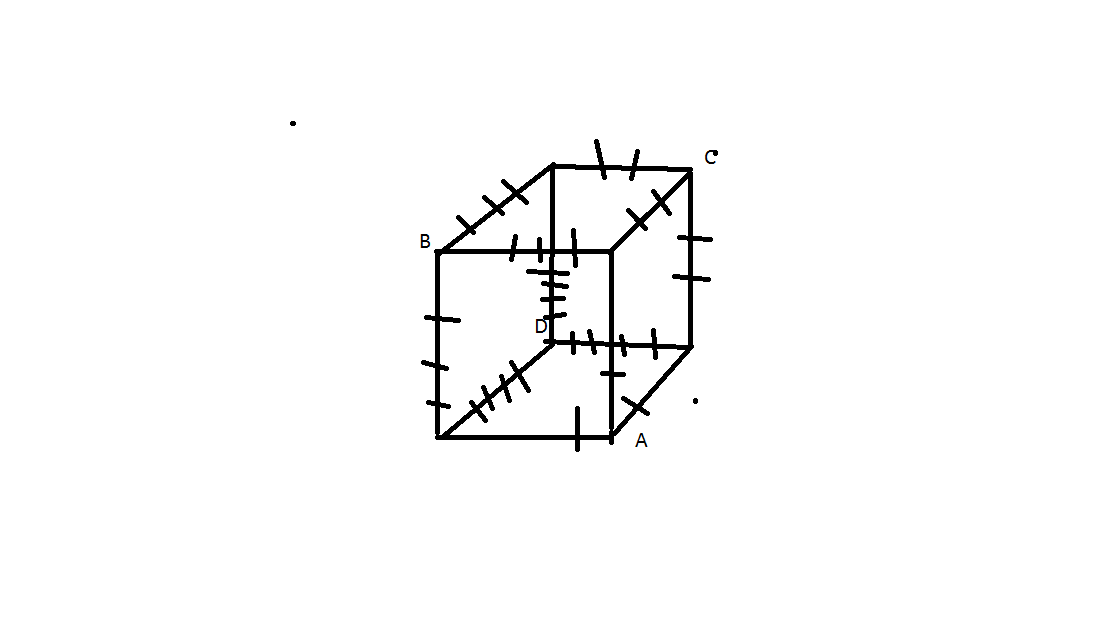
Это можно   понять если посмотреть  на рисунок. На  нем штрихами  обозначены числа при 1  вершине  из вершин A,B,C,D  тк  не  при одной  из этих вершин нет одинаковых  ребер,и  если числа обозначить  только при этих вершинах,то   числа будут  стоять на всех ребрах куба,откуда тк  при всех вершинах   суммы 3   ребер равны,то   сумма   всех чисел равна 4S,то  есть делится на 4. 12   последовательных чисел  можно   представить так:
a;a+1;a+2;a+3;a+4.......a+11  (число  a+11  является двеннадцатым)
тогда их сумма 12a+(1+2+3+4.....+11)=12a+66
число 12a делится на 4,но  тогда раз вся сумма   делится на 4 ,то   раз  12a делится  на 4,то  и 66  должно делится на 4,но   66   не делится на 4. То   есть мы пришли к противоречию. Значит  расставить таким образом числа   нельзя.