Предмет: Математика,
автор: arteomfursov
найдите площадь равнобедренного треугольника изображенного описанного около окружности радиуса: корень из 2
Ответы
Автор ответа:
0
вот в равнобедренном треугольнике высота ВД=h=3*r : медианы в т. пересечения делятся как 1:2, а боковая сторона b - чз радиус вписанной окр.:r=b/(2*(3^(1/2))) , откуда b=r* (2*(3^(1/2))), в прямоуг. треуг.ABD по теореме Пифагора a=(b^2-h^2)^(1/2), тогда все основание: АС=2*a=2*(b^2-h^2)^(1/2), площадь S=1/2*AC*BD=1/2(2*(b^2-h^2)^(1/2))*3*r, после подстановки b получаем S=2r*3*r=6r^2
Приложения:
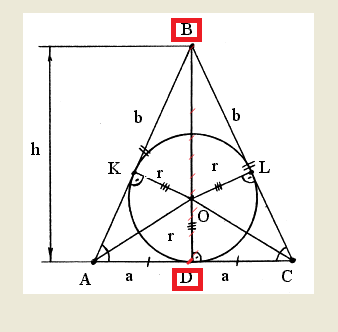
Автор ответа:
0
а радиус r = 2^(1/2), т.е.S=12
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: annagloza
Предмет: Физика,
автор: KatherineOwl
Предмет: Биология,
автор: aardana