Question

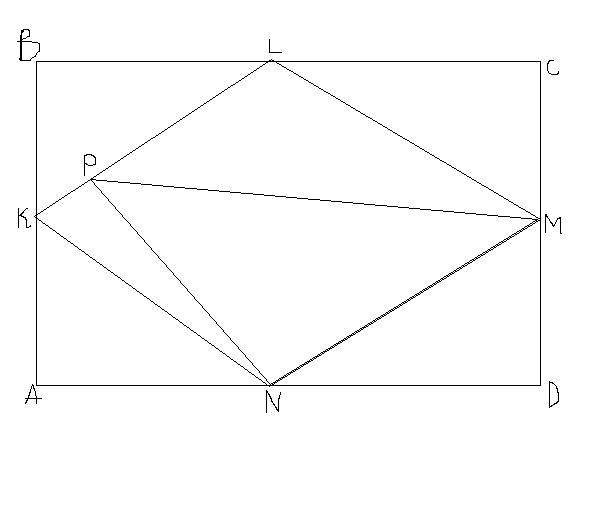
Точки K,L,M,N -середины сторон прямоугольника ABCD,точка P принадлежит отрезку KL,см.рисунок.Площадь треугольника MNP равна 32.Найдите длину стороны BC,если известно,что BC=2AB.
Ответ:16.
Ответ я знаю,а как решать не знаю :(
Помогите пожалуйста !! :)

Answer 1

            
 $BC=2AB\ X=2Y\ KL=sqrt{ frac{x^2}{4}+frac{x^2}{16}}=frac{xsqrt{5}}{4}\ frac{xsqrt{5}}{4} = frac{frac{x}{2}}{sinLKB}\ sinKLB = frac{2}{sqrt{5}}\ LKN=pi-2arccos(frac{1}{sqrt{5}} ) \ S_{NMP} = S_{ABCD}- S_{LMP}- S_{PKN}\ S_{ABCD}= frac{ 5x^2}{16}*sin(pi-2arccos( frac{1}{sqrt{5} })\ S_{LMP} = frac{a*xsqrt{5}}{4}*sin(pi-2arccosfrac{1}{sqrt{5}}*0.5\ S_{PKN} = (frac{xsqrt{5}}{4}-a)*(frac{xsqrt{5}}{4}*sin(2arccos( frac{1}{sqrt{5}}))*0.5$ 
 откуда   $frac{5}{32} x^2 sin(2arcsin frac{1}{sqrt{5}}) = 32\ 5x^2*frac{4}{5}=32^2\ 20x^2=32^2*5\ 4x^2=32^2\ x=256 \ x=16\ BC=16$ 
  
 $a=KP$

Answer 2

Осмелюсь добавить свой вариант:
Площадь треугольника MNP равна 0,5*NM*LH, гле LH - высота ромба KLMN. (Доказывать, что это ромб, надеюсь, не надо?) Заметим, что эта площадь не зависит от расположения точки Р на отрезке KL. Итак, необходимо найти высоту ромба. Пусть половина стороны АВ (CD) = х. Тогда половина стороны ВС (AD) = 2*х. Площадь прямоугольника АВСD = АВ*AD=2х*4х=8х². Сторона ромба находится по Пифагору и равна √(4х²+х²) = х√5. Площади треугольников АКN,KBL,LCM и MDN равны между собой и равны 0,5*х*2х =х². Тогда их суммарная площадь равна 4х². Площадь ромба KLMN равна разности площадей прямоугольника и четырех треугольников, то есть равна 8х²-4х²=4х². Значит его (ромба) высота равна площади, деленной на сторону, то есть 4х²/(х√5) = (4х)/√5. Тогда площадь треугольника MNP = 0,5*NM*LH = 0,5*х√5*(4х)/√5 = 2*х². Или 32=2х², откуда х=4. Тогда искомая сторона ВС=4*х = 16.
Второй вариант:
Ход решения тот же самый до нахождения площади ромба. Площадь ромба KLMN равна разности площадей прямоугольника и четырех треугольников, то есть равна 8х²-4х²=4х². Далее : Площадь треугольника MNP равна 0,5*NM*LH, где LH - высота ромба KLMN. Значит площадь треугольника MNP равна половине площади этого ромба (которую мы определили), то есть 4х²:2=2х². 2х²=32, откуда х=4, а ВС=16.
Все.

Answer 3

А лучше так: Площадь треугольника MNP равна 0,5*NM*LH, где LH - высота ромба KLMN. Значит площадь треугольника MNP равна половине площади этого ромба (которую мы определили), то есть 4х²:2=2х². 2х²=32, откуда х=4, а ВС=16.