Предмет: Алгебра,
автор: kleptik
Решить уравнение  .
.
Ответы
Автор ответа:
0
Рассмотрим выражение в правой части:

Это лекго получить если рассмотреть квадратный трехчлен -16t²-16t+5, где

Корень х=-4.
Осталось доказать, что он единственный.
Решаем уравнение графически.
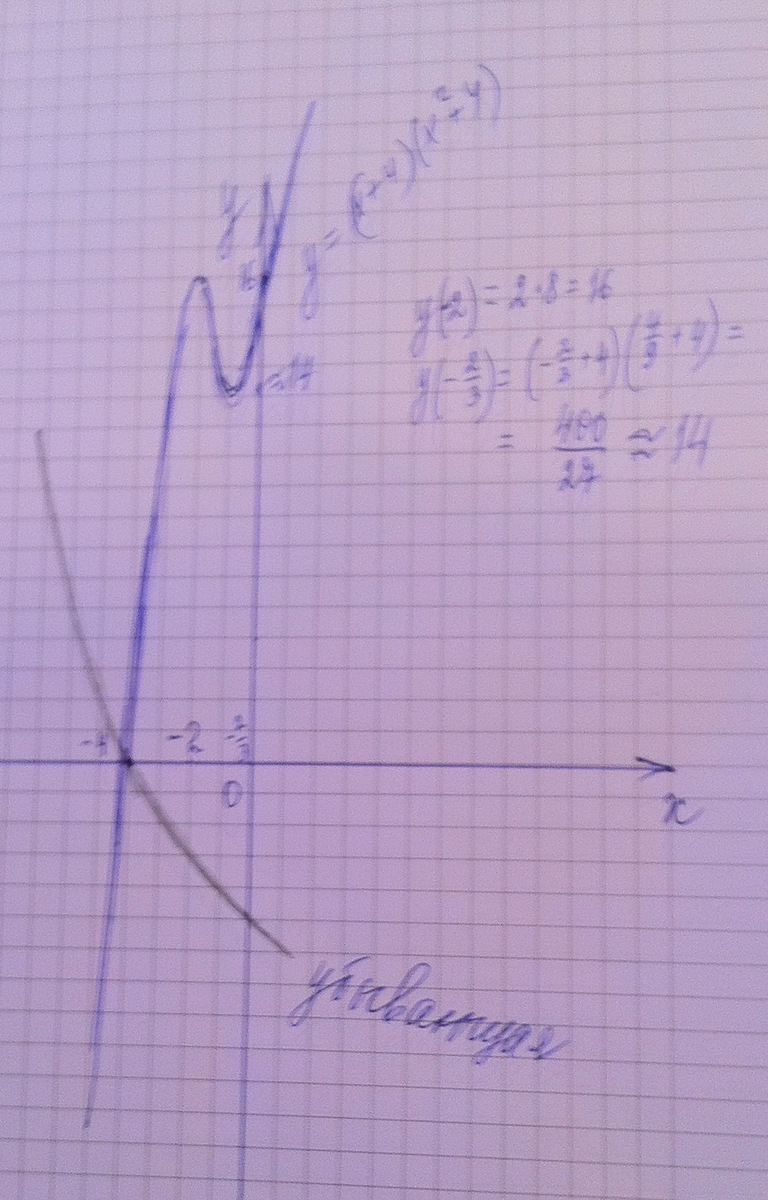
Для этого рассмотрим функцию слева y=(x+4)(x²+4).
Производная у`=x²+4+2x(x+4)=3x²+8x+4
точки возможного экстремума: х=-2 и х=-2/3
Проверив знак производной, убеждаемся, что х=-2 - точка локального максимума, х=-2/3 - точка локального минимума.
Функция пересекает ось ох в точке х=-4
Строим график функции ( см. рисунок)
Исследуем функцию справа:


при любом х, так как показательная функция принимает только положительные значения
значит фугнция справа убывает, пересекает ось ох в единственной точке х=4 и других общих точек с графиком y=(x+4)(x²+4) не имеет
Это лекго получить если рассмотреть квадратный трехчлен -16t²-16t+5, где
Корень х=-4.
Осталось доказать, что он единственный.
Решаем уравнение графически.
Для этого рассмотрим функцию слева y=(x+4)(x²+4).
Производная у`=x²+4+2x(x+4)=3x²+8x+4
точки возможного экстремума: х=-2 и х=-2/3
Проверив знак производной, убеждаемся, что х=-2 - точка локального максимума, х=-2/3 - точка локального минимума.
Функция пересекает ось ох в точке х=-4
Строим график функции ( см. рисунок)
Исследуем функцию справа:
при любом х, так как показательная функция принимает только положительные значения
значит фугнция справа убывает, пересекает ось ох в единственной точке х=4 и других общих точек с графиком y=(x+4)(x²+4) не имеет
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: olgagogol95
Предмет: Окружающий мир,
автор: Аноним
Предмет: Математика,
автор: litvinenkoan