Question

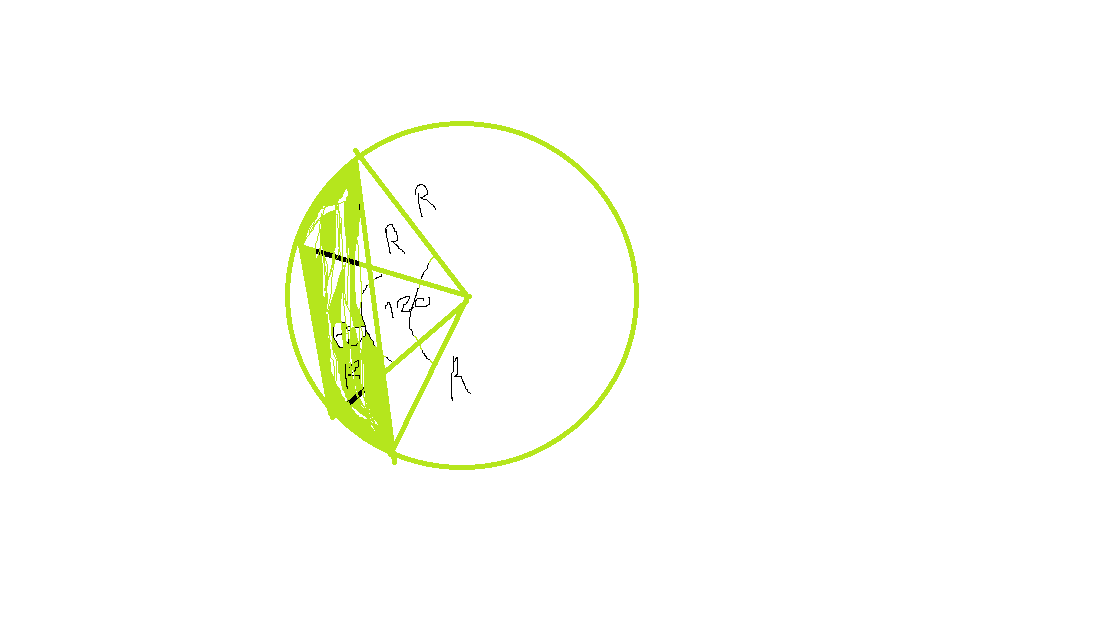
На одной стороне от центра круга радиусом R проведены две параллельные хорды. Найдите площадь между двумя хордами, если их центральные углы равны 120 и 60 градусов

Answer 1

Соединив две  хорды получим трапеция  ,   пусть меньшее  основание равно $AB$ , большее $CD$      
$AB=R$ так как треугольник  $ABO$ равносторонний  
$CD=sqrt{2R^2 -2R^2*cos120}=sqrt{3}R$     
 Найдем высоту трапеций  , по свойству хорд получим 
 $(2R-x)x=(frac{R}{2})^2$  
 $x$  высота сегмента $AB$ 
 $x= frac{(2-sqrt{3})R}{2}$ 
 $(2R-y)y=(frac{sqrt{3}R}{2})^2$ 
 $y$      высота сегмента $AD$ 
   $y=frac{R}{2}$ 
  высота трапеций 
 $H=frac{R-(2-sqrt{3})R}{2} = frac{(sqrt{3}R-1)}{2}$ 
 $S_{trap}=frac{(R+sqrt{3}R)*(sqrt{3}R-1)}{4}$ 
  Найдем площади    сегментов 
  $AC;BD$ 
  $S_{AC}=S_{BD} = R^2arcsin(frac{sqrt{2-sqrt{3}}}{2}) - frac{sqrt{R^2(2-sqrt{3})}}{4}sqrt{4R^2-(R^2(2-sqrt{3}))} =frac{(pi-3)}{12}$ 
 
То есть $frac{(pi-3)R^2}{6}+frac{R^2}{2} = frac{pi*R^2}{6}$
 
 
  

Answer 2

что даю?

Answer 3

Даешь громозкое ,но иетересное решение

Answer 4

Площадь большого сегмента   Это   разность  между всем сектором и прилагающимся треугольником,то же касается малого сегмента
S1=pi*R^2/3 -1/2*R^2*sin120=pi*R^2/3-√3/4 *R^2
S2=pi*R^2/6 -1/2*R^2*sin60=pi*R^2/6-√3/4*R^2
Площадь   закрашенной   части   разность  между площадями  большого  и малого сегментов
S=pi*R^2(1/3-1/6)=pi*R^2/6 
Ответ:1/6 *pi*R^2