Предмет: Геометрия,
автор: Zlatan2014
Площади трапеций, на которые данную трапецию делит средняя линия, относятся как 4:5. Как относятся основания трапеции? Спасибо'
Ответы
Автор ответа:
0
Автор ответа:
0
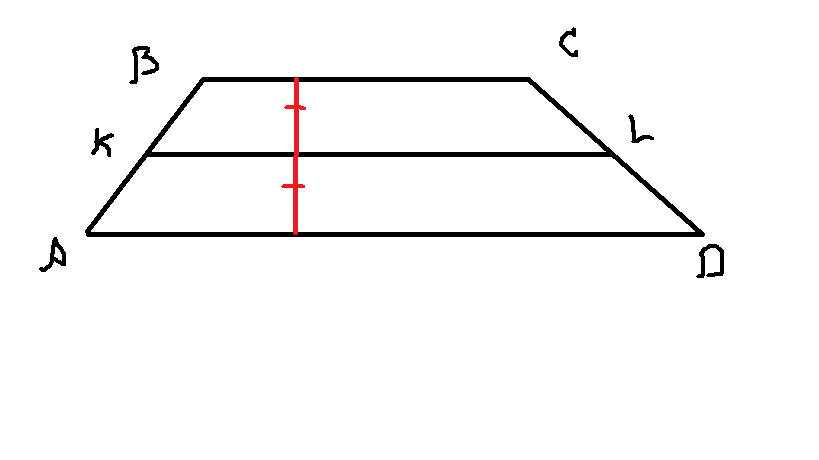
Высота трапеции h (красная) делится средней линией пополам (если непонятно почему - спросите). Тогда запишем площади двух трапеций, точнее я уже запишу с отношением:

Пусть BC=a, AD=b, KL=(a+b)/2. Тогда отношение приобретет вид:

Вам нужно найти a/b. По свойству пропорции это уже легко сделать. Ответ будет 7/11.
Пусть BC=a, AD=b, KL=(a+b)/2. Тогда отношение приобретет вид:
Вам нужно найти a/b. По свойству пропорции это уже легко сделать. Ответ будет 7/11.
Приложения:
Похожие вопросы
Предмет: История,
автор: blacktiger01062000
Предмет: Другие предметы,
автор: vaktar72
Предмет: Математика,
автор: dn4ik009
Предмет: Математика,
автор: аришусик
Предмет: География,
автор: rugalev123