Question

плоскость, проведенная через центр шара, вписанного в конус, параллельна плоскости основания конуса, делит объем конуса пополам. Найти угол при вершине осевого сечения конуса.

Answer 1

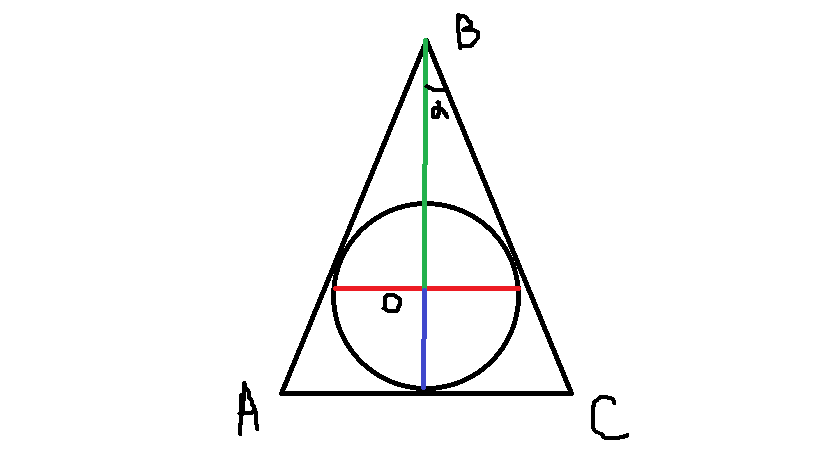
По условию плоскость шара делит объем конуса в отношении 1:1. Она отмечена красной линией. Это значит, что объем всего конуса относится к объему конуса, образованного этой плоскостью как 2/1. Объемы подобных фигур соотносятся как куб коэффициента их подобия. То есть, чтобы перейти к линейным размерам, нужно взять кубический корень нашего отношения. Нас интересует отношение высоты маленького конуса(зеленая) к большой высоте (зеленая+синяя). Получится:
$frac{H-R}{H}=-frac{R}H} +1= frac{1}{ sqrt[3]{2} }$
$frac{R}{H} = frac{ sqrt[3]{2}-1 }{ sqrt[3]{2} }$
Теперь мы знаем как они соотносятся. Нас спрашивают про угол. На моем чертеже это угол альфа, но это только половина искомого. Нетрудно заметить, что его tg=$frac{R}{H-R} = frac{H}{R} -1$. В цифрах это $frac{1}{ sqrt[3]{2}-1 }$. Это только половинный угол. Вам нужно сделать его двойным. Делается это по формуле тангенса двойного угла. Число получилось следующее:$- frac{2}{ sqrt[3]{4} +2}$. Вам нужен теперь арктангенс этого угла. Это и будет ответом.