Question

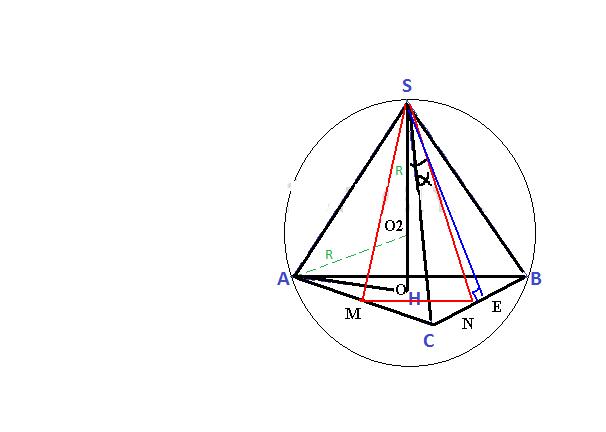
В сферу радиусом √66 вписана правильная треугольная пирамида DABC(D-вершина) длина апофемы которой относится к длине высоты как 3:2 √2 Найдите наименьшую площадь сечения пирамиды плоскостью проходящей через вершину пирамиды середину стороны АС и пересекающей сторону ВС и рисунок

Answer 1

Положим что вершина равна $S$ ,  $SABCD$ правильная  пирамида .
$ABC$     правильный треугольник , тогда обозначим $M$-середину стороны $AC$.  $N in BC$  
Получим сечение $SMN$. 
Положим что угол   $SCE$ равен $alpha=a$ 
$SE$ - апофема. 
$BC=a\ R=sqrt{66}$ 
Из прямоугольного треугольника $SEC\ SC=frac{a}{2sina}\ SE=sqrt{frac{a^2}{4sin^2a}-frac{a^2}{4}}=frac{a*ctga}{2}$         
$O$ центра вписанной окружности в основание $ABC$ , тогда по формуле $OE=r=frac{sqrt{3}a}{6}$  
$OB=R=frac{asqrt{3}}{3}$.
Высота пирамиды$SO$ совпадает  с центром вписанной окружности     
$SH = sqrt{frac{a^2*ctg^2a}{4} - frac{3*a^2}{36}} = frac{asqrt{9*ctg^2a-3}}{6}$ 
По условию
$frac{SE}{SO}=frac{3}{2sqrt{2}}$  
$frac{ frac{a*ctga}{2} }{ frac{a sqrt{9 ctg^2a-3}}{6}} = frac{3}{2sqrt{2}} \\ a=frac{pi}{6}+pi*n ninN$ 
То есть это Тетраэдр. 
Из радиус  сферы получим     по теореме  Пифагора 
 $(frac{asqrt{3}}{3})^2+(sqrt{frac{2}{3}}*a-sqrt{66})^2=sqrt{66}^2\ frac{3a^2}{9}+frac{2a^2}{3}-2asqrt{44}=0\\ 9a^2=18asqrt{44}\\ a=4sqrt{11}$ 
Все грани равны $a=4sqrt{11}$ 
Положим что $CN=x$ 
Тогда по теореме косинусов получим 
$ME=sqrt{x^2-2xsqrt{11}+44}\ SM=sqrt{(4sqrt{11})^2-frac{2sqrt{11}}{2}^2} = 2sqrt{33}\ SN=sqrt{x^2-4xsqrt{11}+176}$ 
Зная все стороны найдем    угол   $SMN$  по теореме косинусов , затем выражая синус через косинус получим 
 $sinSMN = sqrt{1-frac{x^2}{12(x^2-2sqrt{11}x+44}}}$ 
 
 Площадь сечения  тогда равна 
 $S_{SMN}=frac{sqrt{x^2-2xsqrt{11}+44}*sqrt{33}*sqrt{1-frac{x^2}{12(x^2-2sqrt{11}x+44}} }{2}\ S_{SMN}=frac{sqrt{121x^2-264sqrt{11}x+5808}}{2}$
У этой функций минимум находится  в точке 
 $x=frac{12}{sqrt{11}}$ 
 $S_{SMN}=4sqrt{66}$